Tableaux des ressources et des emplois

Le tableau entrées-sorties

Le tableau entrées-sorties (TES) est une présentation du système de production mettant en évidence les relations entre les produits et les branches de l'économie. Il repose sur une décomposition par produits du compte de biens et services :

Compte de biens et services

Ressources	Emplois
Production Importations Impôts sur les produits Moins subventions sur les produits	Consommation intermédiaire Consommation finale Formation brute de capital fixe Variation des stocks Acquisitions moins cession d'objets de valeur Exportations

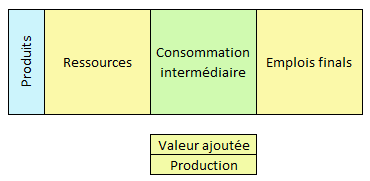
Le TES se présente sous la forme de trois grands blocs :

• une matrice des ressources ventilant par produits les ressources du compte de biens et services ;
• une matrice des consommations intermédiaires ventilée par produits et branches, elle est associée à une matrice ventilant par branches la valeur ajoutée et la production ;
• une matrice des emplois finals ventilant par produits les emplois finals du compte de biens et services.

Une branche est un regroupement d'unités élémentaires de production. Dans le système des comptes, deux conceptions des branches sont définies :

• la branche d'activité qui regroupe les unités d'activité économique au niveau local exerçant la même activité économique principale ; une branche d'activité peut avoir des activités secondaires différentes ;
• la branche homogène qui constitue un regroupement d'unités de production homogène, c'est-à-dire des unités produisant un seul produit ; les unités de production homogène ne sont généralement pas observées directement mais reconstituées à partir de données statistiques.

Les comptes nationaux français utilisent les branches homogènes si bien qu'ils ne décomposent pas la production par branches dans la matrice des ressources. En effet, du fait de la correspondance biunivoque entre branches homogènes et produits, la ventilation par produits est suffisante.

Dans les pays qui utilisent les branches d'activité, la production sera ventilée par branches d'activité et par produits car une même branche d'activité peut avoir plusieurs produits.

Le choix des nomenclatures

Une difficulté pour l'analyse du système productif est la détermination du niveau de finesse auquel il est pertinent de travailler. Un niveau trop fin nécessite de travailler avec des TES énormes difficiles à utiliser et, surtout, les données utilisées risquent d'être trop imprécises car, en statistique, l'imprécision s'accroît avec le niveau de détail. Un niveau trop agrégé risque, au contraire, de cacher certains phénomènes en regroupant des activités trop différentes. Finalement, les comptables nationaux vont travailler à un niveau qui représente un compromis et qui dépend des particularités du pays étudié.

L'analyse des relations entre branches

Pour simplifier l'exposé, nous supposerons que les comptables nationaux ont défini trois branches homogènes : l'agriculture, l'industrie et les services. Au niveau national, il est intéressant de montrer les relations entre ces trois branches. Chacune des branches utilise pour sa consommation intermédiaire des produits provenant des autres branches. Par exemple, l'agriculture utilise des engrais provenant de l'industrie et des services comme des services de location ou des services vétérinaires. L'agriculture utilise elle-même ses propres produits comme consommation intermédiaire, par exemple les semences.

Ces relations peuvent être montrées dans un tableau de synthèse faisant apparaître pour chaque branche la nature des consommations intermédiaires. Ce tableau est la matrice des consommations intermédiaires dont un exemple numérique simple est présenté ci-dessous :

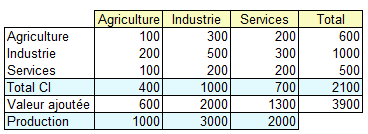
Dans ce tableau les colonnes correspondent aux branches et les lignes aux produits. Ainsi, si nous considérons la colonne "Agriculture", 100 représente la consommation intermédiaire de la branche agriculture en produits de l'agriculture, 200 la consommation intermédiaire de la branche agriculture en produits de l'industrie, 100 la consommation intermédiaire de la branche agriculture en produits des services, 400 est le total de la consommation intermédiaire de la branche agriculture.

Si nous considérons la ligne "Industrie", 200 est la consommation intermédiaire en produits de l'industrie par la branche agriculture, 500 la consommation intermédiaire en produits de l'industrie par la branche industrie, 300 la consommation intermédiaire en produits de l'industrie par la branche des services, 1000 le total de la consommation intermédiaire en produits de l'industrie de l'ensemble de l'économie.

Ce tableau peut être complété par deux autres pour faire apparaître l'ensemble du compte de biens et services. Ainsi, à gauche nous pouvons ajouter un tableau montrant les ressources du compte de biens et services, c'est-à-dire la production, les importations, les impôts moins les subventions sur les produits. Pour simplifier la présentation de notre exemple numérique, nous supposerons qu'il n'y a ni impôts ni subventions sur les produits.

A droite, nous pouvons ajouter un tableau montrant les différents emplois finals, c'est-à-dire la consommation finale, la formation brute de capital fixe, les variations de stocks, les acquisitions de biens de valeur et les exportations. Pour simplifier la présentation nous négligerons les variations de stocks et les acquisitions de biens de valeur.

Nous obtenons ainsi un tableau appelé tableau entrées-sorties (TES) par les comptables nationaux français. Ce tableau est directement tiré des travaux de l'économiste W. Léontieff qui avait publié en 1939 un tableau similaire présentant le système de production des Etats-Unis. Sous une forme très simplifiée, le tableau entrées-sorties se présente sous la forme suivante :

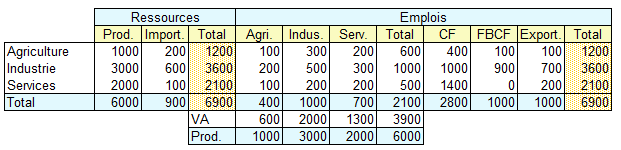
Chaque ligne de ce tableau montre les ressources et les emplois de chaque groupe de produits.

La production se retrouve à la fois dans la première colonne et dans la dernière ligne, dans la colonne il s'agit de la production par produits et dans la ligne il s'agit de la production par branches. Dans notre exemple numérique nous retrouvons les mêmes valeurs parce que nous avons supposé que les branches sont homogènes, c'est-à-dire que chaque branche ne produit qu'un seul produit.

Les marges de commerce et de transport

Très souvent, les clients n'achètent pas les biens et les services directement auprès des producteurs mais passent par l'intermédiaire de commerçants. Ainsi, le prix payé par le client final diffère-t-il généralement du prix payé au producteur d'une marge de commerce. Ceci nous amène à préciser la définition et le calcul de la production des services du commerce.

Par définition, un commerçant achète des biens pour les revendre sans les transformer, il diffère en cela des autres producteurs qui détruisent des biens ou des services (la consommation intermédiaire) pour en produire d'autres. Le commerçant ne détruit pas les biens qu'il achète, il se contente de les revendre dans le même état qu'il les a achetés. Ainsi, les achats de biens par les commerçants ne peuvent pas être considérés comme correspondant à une consommation intermédiaire et, par voie de conséquence, la production de services de commerce ne peut être assimilée au chiffre d'affaires.

La comptabilité nationale définit la production des services du commerce par la marge réalisée sur les ventes, c'est-à-dire la valeur des ventes moins leur coût d'acquisition. Le coût d'acquisition est ici le coût de remplacement, c'est-à-dire le coût d'acquisition des biens vendus si le commerçant devait les acquérir au moment de la vente.

Lorsque nous cherchons à établir l'équilibre ressources-emplois d'un produit particulier, c'est-à-dire le compte de biens et services pour ce produit particulier, nous devons donc tenir compte de marges de commerce. Par exemple, si nous considérons un produit comme l'automobile, la valeur des achats des clients correspond non seulement à la valeur de la production des constructeurs, mais également à la valeur des marges de commerce. Un équilibre ressources-emplois se présente alors sous la forme suivante :

Equilibre ressources-emplois

Ressources	Emplois
Production	Consommation intermédiaire
Importations	Consommation finale
Impôts sur les produits	Formation brute de capital fixe
Moins subventions sur les produits	Variation des stocks
Marges de commerce	Acquisitions moins cessions d'objets de valeur
	Exportations

L'équilibre ressources-emplois correspondant aux services de commerce est assez particulier puisqu'il y a une production mais pas d'emplois. La valeur des services de commerce est, en effet, incluse dans la valeur d'acquisition des autres produits. Aussi, pour assurer l'équilibre, la production est compensée par une marge négative. Le tableau entrées-sorties se présentera alors de la manière suivante :

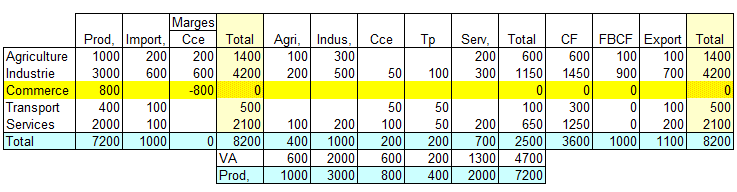
Il est également nécessaire de tenir compte des marges de transport. Les coûts de transport entre le producteur et l'acquéreur sont un élément du coût d'acquisition. La comptabilité nationale distingue trois cas :

• Les coûts de transport sont inclus dans le prix de base de la production lorsqu'ils ne sont pas facturés séparément à l'acquéreur. Ils constituent alors également une consommation intermédiaire du producteur en services de transport.
• Les coûts de transport sont inclus dans la marge de commerce lorsqu'ils ne sont pas facturés séparément à l'acquéreur par le commerçant. Ils constituent alors également une consommation intermédiaire du commerçant en services de transport.
• Les coûts de transport constituent des marges de transport lorsqu'ils sont facturés séparément à l'acquéreur.

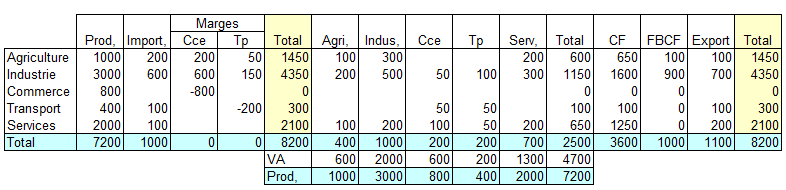
Les marges de transport doivent, comme les marges de commerce, être ajoutées à la production dans l'équilibre ressources-emplois d'un produit. Elles doivent également être traitées de la même manière que les marges de commerce, c'est-à-dire apparaître négativement dans l'équilibre ressources-emplois des services de transport. Le tableau entrées-sorties se présentera alors de la manière suivante :

La correction territoriale

Les notions d'importation et d'exportation correspondent en comptabilité nationale à des échanges entre résidents et non résidents et ne font pas référence au passage de la frontière douanière. Ainsi, la consommation finale des ménages résidents hors du territoire national correspond à une importation de biens et services, de même, la consommation finale des ménages non résidents sur le territoire économique est une exportation. Dans ces deux cas, ce sont non les produits mais les ménages qui se déplacent.

Cela pose un problème au niveau du tableau entrées-sorties car les seules statistiques détaillées par produits portant sur le commerce extérieur sont les statistiques douanières. Or, ces statistiques n'enregistrent les importations et les exportations qu'à l'occasion du franchissement de la frontière douanière. Il n'est donc pas possible, du point de vue statistique, de ventiler par produits la consommation finale des résidents hors du territoire économique national et celle des non-résidents sur le territoire économique national.

Dans ces conditions, les équilibre ressources-emplois par produits du tableau entrées-sorties n'enregistrent dans les importations et les exportations que les biens et services ayant franchi les frontières douanières et la consommation finale qu'ils présentent est celle de l'ensemble des ménages sur le territoire économique national, que ces ménages soient ou non résidents.

Une écriture corrective est alors nécessaire pour retrouver la consommation finale des ménages résidents telle qu'elle apparaît au niveau du compte des ménages et du tableau économique d'ensemble. Ceci est fait en introduisant dans le tableau entrées-sorties une ligne supplémentaire intitulée "correction territoriale".

Les équilibres ressources-emplois par produits du TES correspondent en fait à l'équilibre suivant :

Importations douanières + production = consommation intermédiaire + consommation finale sur le territoire économique + investissement + exportations douanières

Cette équation signifie simplement que les produits disponibles sur le territoire économique ont été soit produits sur ce territoire, soit proviennent d'autres territoires, c'est-à-dire correspondent à des importations douanières. Ces produits ont été soit utilisés sur le territoire économique, soit sortis du territoires, c'est-à-dire exportés au sens des douanes.

La consommation finale sur le territoire économique national est égale à la somme de la consommation finale des ménages résidents et non-résidents sur le territoire économique.

Importations sur le territoire économique	Consommation finale sur le territoire économique		Consommation finale des résidents sur le territoire économique
Production
			Consommation finale des non-résidents
	Consommation intermédiaire
	Formation brute de capital fixe
	Variation des stocks
	Exportations du territoire économique

Pour retrouver les définitions du tableau économique d'ensemble, il convient d'ajouter aux importations la consommation finale hors du territoire économique des ménages résidents et d'ajouter aux exportations la consommation finale des ménages non-résidents sur le territoire économique.

Au niveau de la consommation finale, pour retrouver la consommation finale des ménages résidents, il faut ajouter à la consommation finale sur le territoire économique la consommation finale hors du territoire économique des ménages résidents et déduire la consommation finale des non-résidents sur le territoire économique.

La consommation finale des ménages résidents en dehors du territoire économique est portée dans la ligne "correction territoriale" en importations. La consommation sur le territoire économique des non-résidents est portée dans la ligne "correction territoriale" en exportations.

L'équilibre de la ligne est assuré en ajoutant le solde, c'est à dire la différence entre la consommation finale des ménages résidents en dehors du territoire économique et celle des non-résidents sur le territoire économique, dans la colonne consommation finale. Ainsi, le total de la colonne "consommation finale" correspond bien à la consommation finale des résidents telle qu'elle apparaît dans leurs comptes. En effet ce total est égal à :

Consommation finale sur le territoire économique
− consommation finale des non résidents sur le territoire économique
+ consommation finale des résidents hors du territoire économique

Puisque la consommation finale sur le territoire économique national est égale à la somme de la consommation finale des ménages résidents et non-résidents sur le territoire économique, on constate que la somme de la colonne est égal à :

Consommation finale des ménages résidents sur le territoire économique national
+ consommation finale des ménages résidents hors du territoire économique national
= consommation finale totale des ménages résidents.

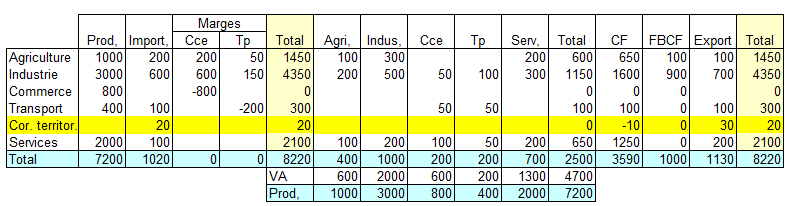
Par exemple, si la consommation finale des ménages résidents hors du territoire économique national est de 20 et la consommation des non résidents sur le territoire économique national est de 30, les écritures dans le tableau entrées-sorties sont les suivantes :

La correction CAF/FAB

La ventilation par produits des importations n'est connue que par les statistiques douanières, or celles-ci évaluent les importations non à leur prix à la frontière du pays exportateur (prix FAB) comme le recommande le système, mais par leur valeur à la frontière nationale, c'est-à-dire au prix CAF. La différence avec le prix FAB correspond au coût d'acheminement des biens de la frontière du pays exportateur à la frontière nationale, c'est-à-dire essentiellement des coûts de transport et, accessoirement, des frais d'assurance. Dans le TES, les importations par produits sont donc mesurées CAF.

Une correction, égale aux frais de transport et d'assurance du point FAB au point CAF, au TES est nécessaire pour que le total des importations de biens soit bien égal au prix FAB. Une ligne et une colonne correspondant à cette correction CAF/FAB sont ainsi introduites dans le TES :

• sur la ligne supplémentaire, la correction CAF/FAB est introduite négativement dans la colonne des importations pour que le total des importations de biens soit mesuré au prix FAB ;
• dans la colonne supplémentaire, la correction est également introduite négativement, dans les lignes correspondant au transport et à l'assurance. En effet, ces services sont déjà inclus dans la valeur CAF des biens importés ;
• la correction est inscrite sur la ligne d'ajustement CAF/FAB, à l'intersection de la colonne CAF/FAB, afin d'annuler le total de la colonne et celui de la ligne.

 

Le modèle de Léontieff

Le tableau entrées-sorties provient essentiellement des tableaux de l'économiste W. Léontieff. Celui-ci avait analysé l'économie américaine en la décomposant en branches d'activités comme le fait le tableau entrées-sorties. Pour simplifier la présentation, nous utiliserons un petit TES simplifié d'une économie fermée, sans importations ni exportations.

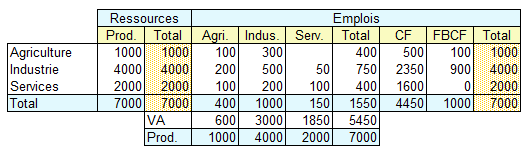
La notion de "coefficients techniques de production" joue un rôle fondamental dans le modèle de Léontieff. Ces coefficients sont obtenus en divisant chaque poste du compte de production détaillé par la valeur de la production. Ils représentent la part de chaque poste de coûts dans le total de la production. Par exemple, pour la branche "Agriculture" les coefficients techniques sont obtenus en divisant les différents postes de la première colonne par 1000.

Le tableau des coefficients techniques est donc le suivant :

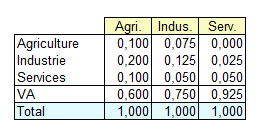
Le modèle de Léontieff repose sur une hypothèse de constance des coefficients techniques, c'est-à-dire par exemple, que pour produire 1€ de produits de l'agriculture, il faut toujours consommer 0,1€ de produits de l'agriculture, 0,2€ de produits de l'industrie et 0,1€ de services. Ceci s'entend, bien entendu, à prix constants car, l'idée de départ est que pour produire une unité d'un bien donné il faut toujours les mêmes quantités de biens intermédiaires. Par exemple, pour produire un pain il faut toujours la même quantité de farine, de sel, de levure, etc.

Ce qui est vrai pour un bien donné reste approximativement vrai pour l'ensemble des biens et services produits par une branche donnée, du moins tant que la structure des productions à l'intérieur de la branche ne varie pas trop. Dans le cas contraire, la stabilité des coefficients techniques n'est plus assurée.

Par exemple, si nous considérons comme branche les industries alimentaires, il est bien évident qu'un arrêt de la production de pain qui serait compensée, en valeur, par une augmentation de la production de bière, verrait la consommation intermédiaire de farine chuter considérablement alors que la production globale de la branche resterait inchangée. Le coefficient technique associé à la farine baisserait donc suite à la modification de la structure de production de la branche.

L'hypothèse de constance des coefficients techniques suppose également une stabilité des techniques de production dans le temps, ce qui n'est jamais totalement vérifié, mais peut raisonnablement être accepté dans des études de court et moyen termes.

Exprimée d'une autre manière, l'hypothèse de stabilité des coefficients techniques signifie tout simplement que si la production double ou triple, alors les consommations intermédiaires et la valeur ajoutée doubleront ou tripleront également.

Les modèles de Léontieff peuvent être utilisés dans deux types d'applications :

• l'étude de l'impact d'une variation de la demande finale d'un produit sur l'ensemble du système de production ;
• l'étude des effets d'une hausse du prix des produits importés ou de celui d'un élément de la valeur ajoutée sur l'ensemble des prix.

Pour étudier l'impact d'une augmentation de la demande finale sur le système de production, supposons, par exemple, que la demande de produits industriels augmente de 400. Pour la satisfaire l'industrie devra augmenter sa production de 400, c'est-à-dire de 10%. Sous l'hypothèse de constance des coefficients techniques cela implique que l'industrie devra également augmenter ses consommations intermédiaires et sa valeur ajoutée de 10%. Le compte de production de l'industrie devient donc :

Branche Industrie

CI agriculture	330
CI industrie	550
CI services	220
CI produits importés : 110
Valeur ajoutée	3300
Production	4400

Ainsi, un accroissement de la production se traduit par une augmentation des consommations intermédiaires des différents produits, c'est-à-dire par une demande supplémentaire qui doit être, elle aussi, satisfaite par un accroissement de la production des branches. Par exemple, la consommation intermédiaire de produits de l'agriculture passe de 300 à 330 ce qui implique que l'agriculture augmente de 30 sa production. Celle-ci étant à l'origine de 1000, il doit y avoir une augmentation de la production de l'agriculture de 3% . Cette augmentation nécessite une augmentation de 3% des consommations intermédiaires de cette branche dont le compte de production devient :

Branche agriculture

CI agriculture	103
CI industrie	206
CI services	103
CI produits importés : 110
Valeur ajoutée	618
Production	1030

Nous voyons que commence un processus où chaque augmentation de la production induit une augmentation des consommations intermédiaires, donc de la demande de produits et par suite un nouvel accroissement de la production. Ainsi, un accroissement de la demande finale, initialement localisé à une seule branche, va se propager à l'ensemble des branches. Ce processus est convergent, c'est-à-dire que les augmentations deviennent de plus en plus petites et que le système finit par se stabiliser à un certain niveau.

Ce problème peut se résoudre mathématiquement. Supposons que, finalement, la production de l'agriculture soit multipliée par un coefficient p1, celle de l'industrie par p2 et celle des services par p3. Puisque nous avons supposé les coefficients techniques constants, l'ensemble du compte de production de chacune des branches sera multipliée respectivement par p1, p2 et p3. La demande finale de produits de l'industrie ayant augmenté de 400, elle passe à 4400. Le TES devient alors :

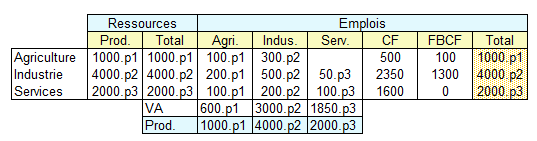
Le total des trois lignes est égal à la production. Nous obtenons ainsi les trois équations suivantes :

100.p1 + 300.p2 + 0.p3 + 600 = 1000.p1

200.p1 + 500.p2 + 50.p3 + 3650 = 4000.p2

100.p1 + 200.p2 + 100.p3 + 1600 = 200.p3

Ce qui donne un système linéaire de trois équations à trois inconnues que l'on peut résoudre facilement, soit en utilisant le calcul matriciel, soit directement en combinant entre elles les différentes équations ou bien encore en faisant appel à des méthodes itératives adaptées à l'usage d'un tableur sur un micro-ordinateur.

Dans notre exemple on trouve les résultats suivants :

p1 = 1,039

p2 = 1,117

p3 =1,014

Ainsi, une augmentation de 10% de la demande de produits industriels a provoqué une croissance de 3,9% dans l'agriculture, de 11,7% dans l'industrie et de 1,4% dans les services. La croissance de l'industrie a finalement été supérieure à 10% car il a fallu satisfaire non seulement directement la demande finale mais également la demande des autres branches qui ont fourni les consommations intermédiaires de l'industrie. Le T.E.S. final s'écrit :

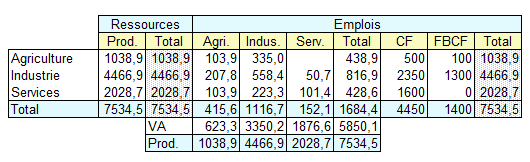
Dans ce modèle nous avons fait l'hypothèse implicite que la production s'alignait instantanément sur la demande, ce qui suppose, en particulier que les capacités de production ne soient pas saturées et que l'excédent de demande ne soit pas satisfait par un déstockage.

Le deuxième type d'utilisation concerne la mesure de l'impact d'une augmentation du prix des produits importés ou de celui d'un élément de la valeur ajoutée sur l'ensemble des prix. Nous traiterons ici le cas d'une augmentation des salaires, celui d'une augmentation du prix des produits importés se traitant de manière très similaire.

Reprenons donc notre exemple initial en supposant que la valeur ajoutée se décompose uniquement en salaires et excédent brut d'exploitation, les comptes de production et d'exploitation des différentes branches se présentant ainsi :

	Agri.	Indus.	Services
Agriculture Industrie Services	100 200 100	300 500 200	0 50 100
Total	400	1000	150
Salaires EBE	200 400	1500 1500	1000 850
VA	600	3000	1850
Production	1000	4000	2000

Supposons que les salaires augmentent de 10% et que les entreprises puissent répercuter intégralement dans leurs prix, c'est-à-dire que leur excédent brut d'exploitation reste inchangé. Nous supposerons également que la production de chaque branche ne varie pas en quantité. Prenons le cas de l'industrie, ses salaires s'élevaient à 1500, après l'augmentation ceux-ci croissent de 150. L'industrie compensera son surcoût de 150 en augmentant de 150 la valeur de sa production qui passera de 4000 à 4150, soit une augmentation de 3,8%.

L'augmentation des salaires induit donc une première augmentation des prix de production dans chaque branche, mais cette première augmentation va se répercuter sur les prix de production de chacune des autres branches par l'intermédiaire des consommations intermédiaires qui verront leur prix croître.

Ainsi, l'augmentation de 3,8% du prix des produits de l'industrie se répercute sur les consommations intermédiaires de chaque branche et provoque une nouvelle augmentation des prix de production des branches concernées. Comme dans le modèle précédent, on assiste à un processus où toute augmentation dans une branche se répercute sur les autres branches. Là encore ce processus est convergent, c'est à-dire qu'il finit par se stabiliser après un certain temps, les augmentations de prix devenant de plus en plus faibles à chaque étape.

Pour résoudre mathématiquement ce modèle nous désignerons par p1,p2 et p3 les coefficients par lesquels sont multipliés, après l'augmentation des salaires, les prix de production d'origine de l'agriculture, de l'industrie et des services. Les salaires ont augmenté de 10% et passent respectivement à 220, 16500 et 1100. Ils ne varieront plus dans la suite du processus sous l'hypothèse que l'augmentation des prix n'a pas de répercussion sur le niveau des salaires. Les comptes de production et d'exploitation finaux s'écrivent :

	Agri.	Indus.	Services
Agriculture Industrie Services	100.p1 200.p2 100.p3	300.p1 500.p2 200.p3	0.p1 50.p2 100.p3
Total	400	1000	150
Salaires EBE	220 400	1650 1500	1100 850
VA	620	3150	1950
Production	1000.p1	4000.p2	2000.p3

Nous obtenons les trois équations suivantes en écrivant que la production est égale à la somme des consommations intermédiaires, des salaires et de l'excédent brut d'exploitation :

100.p1 + 200.p2 + 100.p3 + 220 + 400 = 1000.p1

300.p1 + 500.p2 + 200.p3 + 1650 + 1500 = 4000.p2

0.p1 + 50.p2 + 100.p3 + 1100 + 850 = 2000.p3

Ce système de trois équations à trois inconnues peut se résoudre simplement. Les solutions sont les suivantes :

p1 = 1,039

p2 = 1,0491

p3 = 1,054

Ainsi, une augmentation de 10% des salaires se traduit par une augmentation de 3,9% du prix des produits agricoles, de 4,9 % des produits de l'industrie et de 5,4% des services. Ce modèle est bien entendu très simplifié mais il peut être sophistiqué en modifiant certaines hypothèses de base. Il peut être très utile pour mesurer, par exemple, l'impact mécanique d'une augmentation des prix du pétrole sur les prix intérieurs. Il montre également comment les hausses des prix se répercutent de branche en branche, mettant en évidence, là encore, l'interdépendance de toutes les branches de l'économie nationale.

• Analyse du tableau entrées-sorties symétrique français

Auteur : Francis Malherbe

• Version PDF