L'arbitrage

Le processus d'élaboration des comptes nationaux

Les comptes nationaux sont une sorte de maquette de l'économie d'un pays destinée à servir de support aux analyses macroéconomiques. Pour les réaliser, les comptables nationaux utilisent une multitude de données de base provenant de sources diverses, tout particulièrement des sources administratives et des enquêtes statistiques.

Dans un pays où les données de base seraient parfaites, le travail des comptables nationaux consisterait à compiler ces données de manière à les présenter selon les règles de la comptabilité nationale. En pratique, ce serait essentiellement un travail de nature informatique.

Dans un pays où les données de base seraient rares et peu fiables, le travail du comptable national serait de reconstituer la réalité économique du pays à partir d'indices tout comme un policier le fait pour reconstituer les circonstances d'un crime ou un médecin pour élaborer un diagnostic. C'est à-dire que le travail d'élaboration des comptes serait essentiellement un travail d'analyse et de synthèse.

La réalité d'un pays est toujours intermédiaire :

• les données de base sont trop nombreuses pour être traitées manuellement, si bien qu'une part importante du travail d'élaboration des comptes doit être réalisée par des procédures informatiques ;
• les données ne sont jamais parfaites, elles peuvent être insuffisantes, peu fiables ou même complètement fausses. Le travail du comptable national va donc comporter une grande part d'analyse des données et un important travail de synthèse pour parvenir à ensemble cohérent et fiable.

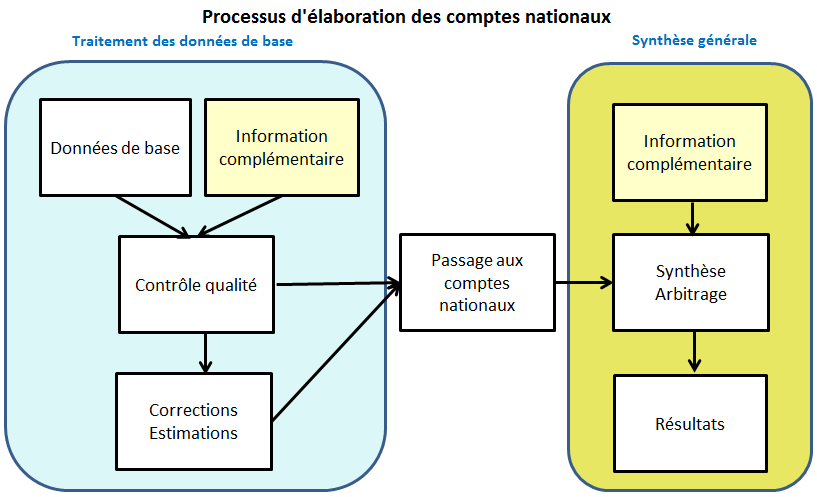
On peut ainsi décrire le processus d'élaboration des comptes nationaux en le décomposant en six phases principales :

• collecte des données de base ;
• contrôle de la qualité de ces données ;
• corrections et estimations complémentaires ;
• passage aux comptes nationaux, c’est-à-dire calcul des agrégats de la comptabilité nationale à partir des données de base ;
• synthèse des résultats dans le cadre central des comptes, c’est-à-dire analyse et mise en cohérence des résultats par arbitrage ;
• publication des résultats selon les normes internationales obligatoires.

Ces six phases peuvent présentées dans le schéma suivant qui distingue les opérations de traitement des données de base et les opérations de synthèse :

Le contrôle de la qualité des données de base

Toutes les données de base doivent être contrôlées car toutes peuvent être fausses. Dans le cas d'une enquête auprès des entreprises, par exemple, l'entreprise peut se tromper parce qu'elle a mal compris la question ou parce qu'elle ne dispose pas directement de l'information demandée. Pour vérifier la validité des données, il est possible de se fonder sur deux principes.

Le principe d'inertie

Le principe fondamental pour la vérification des données est le principe d'inertie. En physique, le principe d'inertie s'exprime ainsi :

Lorsqu'un corps est soumis à des forces qui se compensent ou à aucune force, alors il est soit au repos, soit animé d'un mouvement rectiligne uniforme.

On peut également le présenter en disant que si un corps change de vitesse ou de direction, c'est qu'il est soumis à des forces qui ne se compensent pas.

On peut appliquer ce principe à la vérification des données de base en considérant les évolutions au cours du temps. S'il y a une rupture dans l'évolution d'une série correspondant à une donnée de base, c'est qu'un événement s'est produit. Pour valider l'évolution, il faut alors être capable de déterminer quel est cet événement. De même, s'il n'y a aucune rupture d'évolution dans une série, il faut vérifier qu'aucun événement ne s'est produit qui aurait dû se traduire par une rupture d'évolution.

Le principe d'homothétie ou de rigidité des structures

Le second principe est une variante du principe d'inertie que l'on pourrait appeler le principe d'homothétie ou le principe de rigidité des structures. L'idée est que quand un corps évolue, il tend à garder certaines proportions ou, du moins, que ces proportions n'évoluent que lentement.

Ce principe peut s'appliquer aux entités économiques comme les ménages ou les entreprises. Par exemple, lorsqu'une entreprise se développe, elle accroît son chiffre d'affaires mais, dans le même temps, elle doit certainement augmenter le nombre de ses salariés et donc sa masse salariale. On peut alors penser que le ratio entre le chiffre d'affaires et la masse salariale doit être relativement stable.

Là encore, lorsqu'un ratio caractéristique d'une structure évolue brutalement, on doit pouvoir l'expliquer par un événement particulier.

Les calculs de ratios peuvent être utiles pour vérifier l'évolution au cours du temps mais ils peuvent aussi être utilisés pour repérer des anomalies au sein d'un groupe. Par exemple, on peut penser que les entreprises exerçant la même activité ont des ratios chiffre d'affaires / masse salariale assez proches. Ainsi, si une entreprise présente un ratio très différent des autres, on doit pouvoir expliquer pourquoi.

L'estimation des données manquantes

Les enquêtes n'ont jamais des taux de réponse à 100%, il faut donc estimer les données manquantes. Lorsque les données sont suffisamment nombreuses, la loi des grands nombres peut jouer et l'on peut estimer l'ensemble à partir des réponses exploitables. Mais ce n'est pas toujours le cas, notamment dans les enquêtes auprès des entreprises du fait de l'existence de grandes entreprises dominant leur activité. Si une telle entreprise ne répond pas à l'enquête, il faut alors mobiliser l'information disponible et s'appuyer sur le principe d'inertie et le principe d'homothétie.

Parfois, ce sont des pans entiers de l'économie pour lesquels on ne dispose que de très peu d'informations. Par exemple, les comptables nationaux sont maintenant obligés d'estimer les activités illégales, pourtant il est clair qu'il est vain d'attendre des réponses à une enquête dans ce domaine, les réseaux mafieux étant généralement particulièrement discrets.

L'une des idées fondamentales à la base des comptes nationaux est que, si l'on a besoin d'une maquette de l'économie pour réaliser des analyses macroéconomiques, il faut faire preuve de réalisme. On n'obtiendra jamais toutes les données souhaitables et les données ne seront jamais parfaitement fiables. Il faut donc admettre l'idée qu'une maquette de l'économie ne peut pas être parfaite et qu'exiger la perfection revient à refuser l'idée même d'une maquette.

À partir du moment où l'on pense qu'une maquette de l'économie peut être utile, on comprend alors qu'il serait dommage de renoncer à utiliser des données de bonne qualité sous prétexte qu'elles ne couvrent pas 100% de l'économie mais, par exemple, seulement 90%. Une estimation approximative des 10% manquants est alors préférable à ne rien faire.

De plus, il faut comprendre qu'il est généralement inutile d'avoir des estimations parfaites des comptes nationaux. Par exemple, si l'on cherche à prévoir les recettes fiscales en se basant sur des prévisions du PIB, ces prévisions se baseront sur le lien entre l'évolution du PIB et celle des recettes fiscales et non sur des niveaux. Que le PIB soit systématiquement surévalué ou sous-évalué de 10% n'a ici aucune importance. C'est l'une des raisons pour lesquelles les comptables nationaux mettent davantage l'accent sur les évolutions que sur les niveaux.

Les différents types de cohérence

Après le passage aux comptes des données de base, les comptables nationaux doivent travailler sur des données agrégées. Celles-ci devront respecter des contraintes de cohérence que l'on peut regrouper en trois catégories :

• la première concerne la nécessité d'équilibrer les comptes, c'est elle qui justifie l'appellation "comptabilité" donnée à la comptabilité nationale ;
• la deuxième porte sur la nécessité d'évaluer toujours de la même manière une grandeur qui apparaît dans différents comptes ou tableaux de synthèse ; par exemple, la production totale doit être la même au tableau entrées-sorties et au tableau économique d'ensemble ;
• les contraintes de vraisemblance.

Les contraintes comptables

Les deux premières catégories de contraintes de cohérence peuvent être qualifiées de comptables dans la mesure où elles doivent être respectées à l'unité près.

Les contraintes comptables ne sont jamais respectées spontanément car les opérations qui constituent les comptes sont évaluées à partir de sources indépendantes. Dès lors, deux solutions se présentent aux comptables nationaux pour équilibrer leurs comptes :

• soit ils sélectionnent les données les plus fiables et ils calculent les données les moins fiables par solde ;
• soit ils considèrent qu'aucune donnée n'est totalement fiable et ils vont remettre en cause l'ensemble des opérations du compte à équilibrer, c'est-à-dire qu'ils vont procéder à des arbitrages.

Les arbitrages nécessitent beaucoup de travail et de temps mais ils permettent généralement une meilleure qualité que les estimations par solde.

Les contraintes de vraisemblance

Les contraintes de vraisemblance sont celles qui demandent au comptable national le plus de travail et le plus d'attention. Pour déterminer si un agrégat est vraisemblable ou non, les comptables nationaux peuvent utiliser le principe d'inertie et le principe d'homothétie. Les évolutions constatées à partir des comptes doivent alors être confrontées à des sources externes. Par exemple, l'évolution de la production du bâtiment doit être confrontée à ce que pensent les experts du domaine.

Il faut cependant être conscient qu'un même chiffre peut être regardé selon des points de vue différents et que chaque chiffre publié par les comptables nationaux doit impérativement être vraisemblable selon chacun de ces points de vue.

Par, exemple, si le comptable national publie la consommation intermédiaire en beurre des restaurants, ce chiffre va être examiné à la fois par des producteurs de beurre et par des restaurateurs. Les producteurs de beurre vont voir ce chiffre comme un moyen d'estimer la demande en beurre des restaurants, les restaurateurs pourront comparer la part du beurre dans leur propre consommation intermédiaire à celle qui peut être déduite des comptes nationaux. Ces professionnels sont généralement en mesure d'apprécier, chacun selon ses propres critères, la vraisemblance des estimations proposées par le comptable national.

Les contraintes de vraisemblance peuvent elles-mêmes être décomposées en deux catégories :

• les contraintes de vraisemblance entre données portant sur une même année de comptes ;
• les contraintes de vraisemblance portant sur l'évolution d'une même grandeur au cours du temps.

La vraisemblance des données portant sur une même année est généralement testée soit en comparant différentes composantes des comptes, soit en rapportant les agrégats de la comptabilité nationale à d'autres grandeurs qui lui sont extérieures.

Dans le premier cas, on teste la vraisemblance des structures. Par exemple, en divisant les différents coûts de production d'une branche par la valeur de sa production, on obtient une structure de coûts dont la pertinence peut être appréciée par les professionnels de cette branche.

Dans le deuxième cas, on peut tester la validité des agrégats en les divisant, par exemple, par le nombre d'habitants, le nombre de salariés ou le nombre d'heures travaillées. On peut ainsi calculer le revenu national par habitant ou le salaire moyen par salarié et les comparer aux résultats d'études portant sur le revenu.

Les principales contraintes de vraisemblance sont cependant celles qui portent sur les évolutions parce que, à un certain niveau d'agrégation, les évolutions sont mieux connues que les niveaux. Par exemple, un producteur de beurre ne peut connaître la production totale de beurre de son pays sans consulter les statistiques, mais il connaît l'évolution de sa production, si bien que, s'il consulte quelques collègues et les syndicats professionnels, il peut avoir une idée de la tendance du marché. Pour les opérations sur biens et services, les évolutions doivent être impérativement suivies à la fois en valeur et en volume.

Tous les tests de cohérence doivent être effectués à chaque niveau d'agrégation depuis le plus détaillé jusqu'au plus agrégé. Au niveau le plus agrégé, les comptables nationaux sont amenés à déduire de leurs comptes une véritable analyse de l'évolution économique de leur pays et à confronter cette analyse à celle des économistes. Ils porteront pour cela une attention particulière à l'évolution de certains ratios comme le taux d'épargne ou le taux d'investissement.

Les équilibres ressources-emplois

Les équilibres ressources-emplois fournissent un exemple de la nécessité de l'arbitrage en comptabilité nationale. Ils correspondent à une décomposition par produits du compte de biens et services.

Imaginons donc un comptable national cherchant à élaborer l'équilibre ressources-emplois d'un produit particulier, par exemple le beurre. Supposons que les ressources se résument à la production, les emplois étant limités à la consommation intermédiaire et à la consommation finale.

Supposons, dans un premier temps, que le comptable national dispose de deux sources pour réaliser son équilibre pour le beurre, une enquête auprès des entreprises qui évalue à 100 sa production, et une enquête auprès des ménages qui estime à 80 sa consommation finale. La consommation intermédiaire de beurre correspond principalement à la consommation de beurre par les industries alimentaires et les restaurants, elle peut être estimée par solde de l'équilibre ressources-emplois.

ERE du beurre

Ressources		Emplois
Production	100	Consommation intermédiaire	20
		Consommation finale	80
Total	100	Total	100

Le comptable national peut se satisfaire de cet équilibre mais, s'il est consciencieux, il peut être préoccupé par la fiabilité de son estimation de la consommation intermédiaire. En effet, la production et la consommation finale sont estimées à partir d'enquêtes qui ne peuvent être parfaitement fiables. Or, le calcul par solde a pour conséquence de faire porter sur la consommation intermédiaire toute l'incertitude affectant les estimations de la production et de la consommation finale.

Supposons, par exemple, que les résultats des deux enquêtes soient connus à 2% près. La production est donc comprise entre 98 et 102 et la consommation finale entre 78,4 et 81,6, la consommation intermédiaire est alors comprise entre 98−81,6=16,4 et 102−78,4=23,6, c'est-à-dire avec un écart de 18% par rapport à la moyenne égale à 20.

	Minimum	Maximum
Production	98	102
Consommation finale	78,4	81,6
Consommation intermédiaire	16,4	23,6

Le calcul de la consommation intermédiaire par solde conduit ainsi à une imprécision peu acceptable.

Pour améliorer son estimation, le comptable national peut faire appel à une nouvelle source. Par exemple, il peut interroger un échantillon d'entreprises productrices de beurre et leur demander quelle part de leur production est destinée à la consommation intermédiaire.

Supposons que cette enquête estime à 15% la part de la production de beurre destinée à la consommation intermédiaire. La production étant de 100, cela signifie que l'enquête estime à 15 la consommation de beurre, ou à un intervalle compris entre 14,7 et 15,3 si l'on suppose une incertitude de 2%.

Cette estimation ne recouvre pas celle obtenue par solde. Ce n'est pas vraiment étonnant pour deux raisons. D'une part, les statisticiens raisonnent en termes d'intervalles de confiance, c'est-à-dire qu'il y a, par exemple, 95% de chances que la réalité se situe dans l'intervalle de confiance et 5% qu'elle soit en dehors. On peut très bien avoir la malchance de tomber dans les 5%. Vu le nombre d'estimations utilisées par les comptables nationaux, cela arrive nécessairement fréquemment. D'autre part, certaines sources d'erreurs sont difficiles à estimer, si bien que les intervalles de confiance sont assez approximatifs et parfois très optimistes.

Le comptable national est lié par une contrainte fondamentale : il doit impérativement équilibrer ses comptes à l'unité près. Il va donc devoir arbitrer entre les différentes estimations et, pour cela, analyser la fiabilité des différentes sources, éventuellement faire appel à d'autres sources, ou même consulter l'avis d'experts spécialistes du domaine concerné.

Mais, quels que soient ses efforts, il se trouvera finalement confronté à la nécessité de décider d'une estimation sans pouvoir s'appuyer sur aucune certitude. Pour de jeunes comptables nationaux nourris de certitudes mathématiques, cette décision n'est pas toujours facile à prendre !

Nous touchons ici à la principale spécificité du travail du comptable national.

De cette nécessité d'arbitrage résulte que, non seulement les comptes nationaux ne sont connus qu'avec une certaine incertitude, mais également qu'ils comportent toujours une part de subjectivité, si bien que l'une des préoccupations constantes des comptables nationaux est précisément de mettre en place des procédures leur permettant de réduire le plus possible cette part de subjectivité dans leurs estimations.

La synthèse générale des comptes

Les comptes nationaux comprennent deux grands tableaux de synthèse, le tableau économique d'ensemble, c'est-à-dire le tableau des comptes de secteurs, et le tableau économique d'ensemble. Ces tableaux sont complétés par deux documents de synthèse, le tableau des opérations financières et la balance des paiements.

Le tableau économique d'ensemble

Le tableau économique d'ensemble est le plus riche du point de vue de l'analyse économique car il peut directement être relié à l'analyse financière et aux comptes de patrimoine. Il se présente très schématiquement sous la forme suivante :

Emplois					Ressources
Sociétés	Admin. publiques	Ménages	Reste du monde		Sociétés	Admin. publiques	Ménages	Reste du monde
				Solde extérieur B&S
				Production
				Consommation intermédiaire
				Répartition du revenu
				Consommation finale
				Formation brute de capital
				Capacité de financement

En colonnes, on retrouve les secteurs institutionnels et en lignes les opérations. La capacité de financement est le solde des comptes de secteurs. La propriété fondamentale du tableau économique d'ensemble est que la somme des capacités de financement de l'ensemble des secteurs, y compris le reste du monde, est rigoureusement égale à zéro.

Pour comprendre le travail d'équilibrage que nécessite ce tableau, il peut être utile de regrouper très schématiquement les secteurs institutionnels en deux blocs selon la fiabilité de l'information dont on dispose pour confectionner leurs comptes. On considérera donc un bloc dur, réalisé à partir d'informations relativement fiables et un bloc mou réalisé à partir d'informations moins fiables.

Le bloc dur est constitué des sociétés non financières, des sociétés financières, des administrations publiques et du reste du monde, le bloc mou est constitué des ménages et des institutions sans but lucratif au service des ménages.

La problématique de l'équilibrage peut être visualisée dans le tableau ci-dessous :

Emplois				Ressources
Bloc dur	Bloc mou	Total		Bloc dur	Bloc mou	Total
			Solde extérieur B&S
			Production
			Consommation intermédiaire
			Répartition du revenu
			Consommation finale
			Formation brute de capital
		0	Capacité de financement

Dans ce tableau, les cases de couleur verte correspondent aux informations les plus fiables et les cases de couleur orange correspondent aux informations les moins fiables.

Toutes les opérations du bloc dur sont relativement bien connues, sa capacité de financement l'est donc aussi. Comme la somme des capacités de financement des deux blocs est nulle, la capacité de financement du bloc mou est l'opposé de la capacité de financement du bloc dur, c'est-à-dire qu'elle est également bien connue.

Si l'on raisonne en termes de distribution nette de revenu, c'est-à-dire de différence entre le revenu reçu et le revenu versé, on peut considérer que le bloc dur verse un revenu au bloc mou, si bien que, puisque le revenu versé par le bloc dur est connu, le revenu reçu par le bloc mou l'est aussi.

Ainsi, deux postes du compte du bloc mou sont connus, la capacité de financement et le revenu reçu, ce qui réduit l'incertitude. Le total des deux colonnes du bloc mou étant égales on peut écrire pour ce bloc :

Production + revenu reçu = CI + CF + FBC + capacité de financement

Où CI désigne la consommation intermédiaire, CF la consommation finale, FBC la formation brute de capital.

L'équation peut encore s'écrire :

(Production − CI) + (revenu reçu − capacité de financement) = CF + FBC

C'est-à-dire :

Valeur ajoutée + données connues = consommation finale + formation brute de capital

Equilibre du bloc mou

Valeur ajoutée	Consommation finale
Données connues
	Formation brute de capital

Le schéma ci-dessus montre qu'un arbitrage doit être réalisé entre deux blocs :

• la valeur ajoutée du bloc mou ;
• la somme de la consommation finale et de la formation brute de capital du bloc mou.

Ces deux blocs sont généralement estimés selon deux approches différentes, l'approche production pour la valeur ajoutée, l'approche dépenses pour la consommation finale et la formation brute de capital.

On peut penser que, dans le cadre d'une estimation par secteurs institutionnels, l'approche production est plus fiable que l'approche dépenses et l'on peut donc commencer par une estimation de la valeur ajoutée du bloc mou. Reste alors l'arbitrage le plus difficile, celui qui permet de ventiler les dépenses du bloc mou entre consommation finale et formation brute de capital.

Se contenter d'une analyse au niveau des comptes des secteurs institutionnels revient donc à laisser aux comptables nationaux une grande liberté dans le choix du taux d'épargne des ménages.

Les équilibres ressources-emplois

Pour améliorer la synthèse, il est donc nécessaire d'introduire un deuxième niveau d'arbitrage. Celui-ci aura lieu dans le cadre des équilibres ressources-emplois. L'idée à la base de l'utilisation des équilibres ressources-emplois est que, du fait de leur nature, certains produits sont nécessairement utilisés pour la consommation (intermédiaire et finale) et d'autres pour l’investissement, c’est-à-dire la formation brute de capital. Par exemple, une locomotive est rarement utilisée pour la consommation finale, un œuf peut difficilement participer à la formation de capital fixe.

Ainsi, si l’on est capable de ventiler par produits les opérations sur biens et services de la comptabilité nationale, on obtient une estimation de la formation brute de capital.

Equilibres ressources-emplois par produit

Ressources		Emplois
Production	Importations	Consommation intermédiaire	Consommation finale	Formation brute de capital	Exportations
Produits de consommation		Produits de consommation			Produits de consommation
Produits d'investissement				Solde = Formation brute de capital	Produits d'investissement

En fournissant une estimation de la formation brute de capital, les équilibres ressources-emplois peuvent donc aider les comptables nationaux à effectuer leur équilibrage du tableau économique d'ensemble.

Dans ces conditions, il est clair qu'un équilibrage simultané du tableau économique d'ensemble et des équilibres ressources-emplois apporte davantage de fiabilité qu'une procédure consistant à équilibrer le tableau économique d'ensemble sans utiliser l'information que pourrait apporter les équilibres ressources-emplois.

Le tableau entrées-sorties

On peut aller plus loin et utiliser non seulement les équilibres ressources-emplois mais aussi l'ensemble du tableau entrées-sorties pour améliorer l'équilibrage des comptes. Celui-ci fournit, en effet, également des relations entre la production d'une branche et ses consommations intermédiaires ventilées par produit.

Considérons, par exemple, les équilibres ressources-emplois simplifiés suivants correspondant à une première estimation :

Equilibres ressources-emplois

	Ressources	Emplois
	Prod.	CI	CF	FBCF	Total
Agriculture	1000	200	800		1000
Industrie	5000	2000	2000	1000	5000
Services	2000	500	1500		2000
Total	8000	2700	4300	1000	8000

Supposons que l'on dispose, par ailleurs, des résultats d'une enquête portant sur la structure des coûts des entreprises qui décompose les consommations intermédiaires par produit. Les résultats de cette enquête fournissent un tableau exprimant les consommations intermédiaires de chaque branche en pourcentage de leur production :

	Agri.	Indus.	Services
Agriculture	5	10
Industrie	10	20	5
Services	5	10	5
Total	20	40	10

Dans ce tableau, les branches sont en colonnes et les produits en ligne. Par exemple, la consommation intermédiaire de la branche Agriculture en produits de l'industrie correspond à 10% de la production. Si l'on applique ces coefficients au tableau des équilibres ressources-emplois, on obtient :

	Prod.	Consommations intermédiaires				CF	FBCF	Total
		Agri.	Indus.	Services	Total
Agriculture	1000	50	500	0	550	800		1350
Industrie	5000	100	1000	100	1200	2000	1000	4200
Services	2000	50	500	100	650	1500		2150
Total	8000	200	2000	200	2400	4300	1000	7700

On voit que ce tableau n'est plus équilibré puisque, pour chaque ligne, le total des emplois n'est plus égal aux ressources, il faut donc le modifier en arbitrant entre les différentes sources disponibles.

Trois options sont possibles :

• considérer que les équilibres ressources-emplois étaient corrects et qu'il ne faut pas les modifier, l'équilibrage consistera alors à ventiler les consommations intermédiaires par ligne sans toucher à leur total tout en modifiant le moins possible la structure des coûts donnée par l'enquête ;
• considérer que la structure des coûts de production est la meilleure source et modifier la consommation finale et la formation brute de capital fixe par produit ; il est possible de modifier également la production, ce qui amènera à recalculer les consommations intermédiaires ;
• considérer qu'aucune donnée n'est parfaite et se donner le droit de modifier l'ensemble du tableau de manière à distordre au minimum sa structure, ce qui est généralement la meilleure solution en termes de qualité du résultat.

Notons que seule la première méthode ne modifie pas la valeur ajoutée et ne remet pas en cause un éventuel arbitrage préalable avec le tableau économique d'ensemble.

Si l'on veut obtenir les meilleurs résultats en adoptant la troisième méthode, il est nécessaire de procéder à un arbitrage coordonné et simultané du tableau économique d'ensemble et du tableau entrées-sorties car toute modification apportée à l'un des deux tableaux se répercute sur l'autre. Ce travail d'équilibrage simultané des deux tableaux de synthèse nécessite des moyens importants et une bonne organisation.

Le passage secteurs-branches

Les comptables nationaux français utilisent deux types de regroupements pour analyser le système de production : les secteurs d'activité et les branches d'activité. Les secteurs d'activité regroupent les entreprises ayant la même activité principale, les branches d'activité regroupent les unités de production homogènes, c'est-à-dire des unités produisant un seul produit ou, du moins, des produits appartenant au même item de la nomenclature de produits.

Puisqu'une même entreprise peut produire des produits de catégories différentes, un secteur d'activité comprend généralement plusieurs branches d'activités. Ainsi, à partir des statistiques d'entreprises, il est possible de réaliser une matrice ventilant la production par secteur d'activité et par branche, cette matrice prend le nom de matrice secteurs-branches. Par exemple, la matrice ci-dessous :

Production par secteur d'activité et branche

	B1 - Agri.	B2 - Indus.	B3 - Services	Total
S1 - Agriculture	350	40	5	395
S2 - Industrie	20	750	20	790
S3 - Services	15	130	450	595
Total	385	920	475	1780

Dans cette matrice les lignes correspondent aux secteurs d'activité et les colonnes aux branches. Par exemple, la production du secteur d'activité Agriculture est égale à 395, elle est composée de produits de l'agriculture pour une valeur de 350, de produits de l'industrie pour une valeur de 40 et de services pour une valeur de 5.

De même, en colonne, on voit que les produits de l'agriculture ont été produits pour une valeur de 350 par le secteur d'activité de l'agriculture, pour une valeur de 20 par le secteur d'activité de l'industrie et pour une valeur de 15 par le secteur d'activité des services.

Pour déterminer les consommations intermédiaires des secteurs d'activité et des branches, on fait généralement l'hypothèse d'une technologie produits qui consiste à supposer que la consommation intermédiaire d'une branche est proportionnelle à la production de cette branche et ne dépend pas du secteur considéré. Si l'on accepte cette hypothèse, il est possible de passer des consommations intermédiaires des branches à celles des secteurs et inversement. On utilisera, pour cela, la matrice de structure déduite de la matrice secteurs-branches, elle se présente comme suit :

Ventilation de la production des branches par secteur d'activité

	B1 - Agri.	B2 - Indus.	B3 - Services
S1 - Agriculture	0,9091	0,0435	0,0105
S2 - Industrie	0,0519	0,8152	0,0421
S3 - Services	0,0390	0,1413	0,9474
Total	1,0000	1,0000	1,0000

Cette matrice donne la répartition de la production d'une branche selon les secteurs d'activité. Par exemple, la production de la branche Agriculture provient pour 90,91% du secteur d'activité de l'agriculture, pour 5,19% de celui de l'industrie et pour 3,90% de celui des services.

Puisque l'on a supposé une technologie produits, cette matrice donne également la répartition de la consommation intermédiaire des branches selon les secteurs d'activité. En effet, pour une branche déterminée, le ratio entre la consommation intermédiaire et la production est le même pour tous les secteurs d'activité si bien que la consommation intermédiaire et la production d'une branche sont proportionnelles. Elles ont donc la même répartition par secteur d'activité.

Supposons, par exemple, que l'on connaisse les consommations intermédiaires des branches, celles-ci étant présentées dans la matrice suivante :

Consommation intermédiaire

Branches	CI
B1 - Agriculture B2 - Industrie B3 - Services	90 410 80

Si l'on désigne par ST la matrice de structure secteurs-branches, par CB la matrice des consommations intermédiaires des branches et par CS celle des consommations intermédiaires des secteurs, on a :

CS = ST × CB

On trouve :

Consommation intermédiaire

Secteurs	CI
S1 - Agriculture S2 - Industrie S3 - Services	100,5 342,3 137,2

En effet, par exemple, la consommation intermédiaire du secteur Agriculture est égale à 90,91% de la consommation intermédiaire de la branche Agriculture plus 4,35% de la consommation intermédiaire de la branche Industrie plus 1,05% de la consommation intermédiaire de la branche Services, c'est-à-dire :

0,9091 × 90 + 0,0435 × 410 + 0,0105 × 80 = 100,5

Cependant, en général, les statistiques d'entreprises fournissent les consommations intermédiaires par secteur d'activité et il est nécessaire de calculer les consommations intermédiaires par branche pour pouvoir élaborer le tableau entrées-sorties. On déduit donc de l'équation matricielle précédente :

CB = ST^-1 × CS

Où ST^-1 est l'inverse de la matrice ST. On peut vérifier que si l'on applique cette équation aux consommations intermédiaires des secteurs d'activité précédemment calculées, on retrouve bien les consommations intermédiaires des branches.

Comptes financiers et balance des paiements

Habituellement, les comptes nationaux ne sont pas réalisés par une seule mais par trois équipes :

• une équipe en charge des comptes non financiers des secteurs institutionnels ;
• une équipe en charge des comptes financiers des secteurs institutionnels ;
• une équipe en charge de la balance des paiements, c'est-à-dire des comptes du reste du monde.

Ces trois équipes ne peuvent pas travailler indépendamment car elles sont liées par des relations qui, en théorie, doivent être vérifiées à l'unité près :

• la capacité de financement est à la fois le solde des comptes non financiers et le solde des comptes financiers ;
• la somme des capacités de financement des secteurs institutionnels est égale au besoin de financement du reste du monde.

Ces contraintes ne sont pas sans conséquence sur le travail d'équilibrage des comptes nationaux.

Comptes non financiers et comptes financiers

Nous avons vu qu'une synthèse de qualité des comptes non financiers exigeait un travail simultané sur le tableau économique d'ensemble et le tableau entrées-sorties. Habituellement, ces tableaux sont réalisés par deux équipes différentes qui travaillent en étroite collaboration et réalisent ensemble l'arbitrage général. Lorsqu'elles parviennent à un accord, c'est nécessairement sur un équilibre au niveau global parce que les équilibres ressources-emplois ne sont pas décomposés par secteur institutionnel.

L'équipe en charge du tableau économique d'ensemble va alors devoir répartir les estimations des opérations sur biens et services résultant de l'arbitrage entre les différents secteurs institutionnels. Ensuite, ils effectueront la ventilation des opérations de répartition (rémunération des salariés, revenus de la propriété, etc.) et feront apparaître pour chaque secteur institutionnel la capacité de financement. Ce processus peut être décrit très schématiquement de la manière suivante :

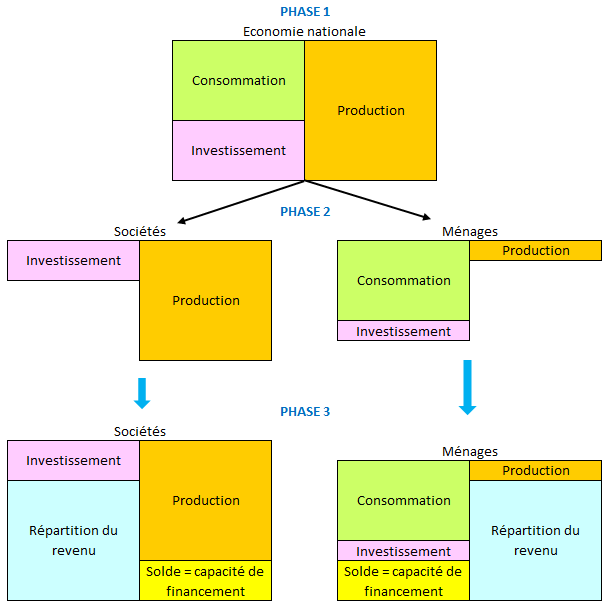
Nous avons considéré ici, pour simplifier, le cas d'une économie fermée composée de deux secteurs institutionnels : les sociétés et les ménages. Les consommations intermédiaires ont été négligées et l'investissement correspond à la formation brute de capital.

Les capacités de financement déterminées à l'issue de ce processus sont alors confrontées aux capacités de financement issues des comptes financiers. Puisque ce travail est réalisé par deux équipes indépendantes, il y a toujours un écart entre les capacités de financement provenant des deux séries de comptes. Cet écart est parfois loin d'être négligeable et il faut alors commencer un processus d'arbitrage entre l'équipe en charge des comptes non financiers et celle en charge des comptes financiers.

À ce stade deux approches sont possibles :

• la première consiste à considérer que l'arbitrage entre l'équipe en charge du tableau économique d'ensemble et celle en charge du tableau entrées-sorties a été long et difficile à obtenir, si bien qu'il ne faut pas y toucher. Les seules modifications possibles au niveau du tableau économique d'ensemble portent alors sur les opérations de répartition ;
• la seconde consiste à considérer qu'aucune mesure n'est parfaite et qu'on modifiera moins la structure des comptes en répartissant l'écart constaté sur l'ensemble des opérations et non seulement sur les opérations de répartition. Il faut alors revenir sur l'accord trouvé entre l'équipe en charge du tableau économique d'ensemble et l'équipe en charge du tableau entrées-sorties.

On peut illustrer les deux méthodes à l'aide d'un exemple numérique où nous supposons qu'un écart de 500 existe entre les estimations de la capacité de financement des sociétés provenant des deux séries de comptes.

	Avant arbitrage	Après arbitrage
		Méthode 1	Méthode 2
Production	9000	9000	8775
Investissement	2000	2000	2050
Répartition du revenu	9000	9500	9225
Capacité de financement	-2000	-2500	-2500
Ecart	-500	0	0

Dans la première méthode, l'écart a été reporté uniquement sur les opérations de répartition, dans la deuxième méthode il a été réparti proportionnellement sur chaque poste.

On voit ici que la deuxième méthode perturbe moins la structure des comptes, si bien qu'elle est préférable, mais elle nécessite d'associer le plus tôt possible l'équipe en charge des comptes financiers aux deux équipes en charge des comptes non financiers, elle prend plus de temps et exige plus de travail.

La balance des paiements

La balance des paiements est très souvent réalisée indépendamment des comptes nationaux par une équipe de la banque centrale qui travaille sous le contrôle du Fonds monétaire international. Le problème est que la balance des paiements est aussi le compte du reste du monde de la comptabilité nationale et qu'elle lui est liée par la relation entre les capacités de financement.

Comme tout document statistique, la balance des paiements n'est pas exempte d'incertitude. Si les comptables nationaux sont obligés d'accepter sans modification possible la balance des paiements comme étant leur compte du reste du monde, l'incertitude est reportée sur les comptes de secteurs, ce qui peut poser des problèmes pour les pays largement ouverts sur l'extérieur.

L'idéal serait ici que l'élaboration des comptes de secteurs institutionnels et de la balance des paiements soit réalisée conjointement par l'ensemble des équipes en charge des comptes nationaux. Mais il n'est pas certain que cet idéal puisse être atteint dans la majorité des pays avant quelques années.

Le niveau de détail

La fiabilité des comptes nationaux repose largement sur la multiplication des contrôles de cohérence, ce qui implique que l'un des meilleurs moyens dont disposent les comptables nationaux pour améliorer leurs estimations est de travailler à un niveau fin.

Supposons, par exemple, que le comptable national cherche à estimer la formation brute de capital fixe des entreprises de transport en matériel de transport et qu'il dispose pour cela de deux évaluations, la première tirée des équilibres ressources-emplois, la seconde des comptes des entreprises.

Nous supposerons que le matériel de transport correspond à trois produits pour lesquels il existe des équilibres ressources-emplois :

• les voitures ;
• les camions ,
• les avions.

Nous supposerons que les entreprises de transport recouvrent trois branches :

• les taxis ;
• les transporteurs routiers ;
• les compagnies aériennes.

Nous supposerons également, pour simplifier, que seules les entreprises de transport investissent dans du matériel de transport.

Les équilibres ressources-emplois donnent des estimations par produit de la formation brute de capital fixe pour l'ensemble de l'économie, c'est-à-dire dans notre exemple simplifié pour l'ensemble des entreprises de transport. Ces estimations sont les suivantes :

FBCF en matériel de transport

Produits	FBCF
Voitures Camions Avions	2000 2000 1000
Total	5000

Les comptes des entreprises donnent la valeur de la formation brute de capital fixe en matériel de transport par branche mais sans donner de décomposition par produit, par exemple :

FBCF en matériel de transport

Branches	FBCF
Taxis Transporteurs routiers Compagnies aériennes	1000 2000 1000
Total	4000

Puisque les estimations résultant des équilibres ressources-emplois et des comptes d'entreprises diffèrent, le comptable national doit réaliser un arbitrage. S'il considère que les équilibres ressources-emplois sont beaucoup plus fiables que les comptes des entreprises, il peut décider de retenir 5000 comme estimation de la formation brute de capital fixe de l'ensemble des entreprises en matériel de transport et de ventiler ce chiffre proportionnellement aux estimations par branche que donnent les comptes d'entreprises. Il obtient :

FBCF en matériel de transport

Branches	FBCF
Taxis Transporteurs routiers Compagnies aériennes	1250 2500 1250
Total	5000

Mais il peut également remarquer que les taxis investissent principalement en voitures, les transporteurs routiers en camions et les compagnies aériennes en avions. Il peut donc penser que le tableau suivant qui croise produits et branches lui donne une estimation plus vraisemblable :

	Voitures	Camions	Avions	Total
Taxis Transporteurs routiers Compagnies aériennes	2000 0 0	0 2000 0	0 0 1000	2000 2000 1000
Total	2000	2000	1000	5000

Les estimations de la formation brute de capital fixe par branche sont différentes des précédentes mais on peut penser qu'elles sont meilleures car elles tiennent compte d'une information supplémentaire qui est la structure par produits de la formation brute de capital fixe dans les différentes branches.

Mais le comptable national peut penser que son tableau est trop caricatural car, par exemple, les compagnies aériennes peuvent investir non seulement en avions mais également en voitures. Comme il ne dispose d'aucune information sur l'investissement en voitures des compagnies aériennes, le comptable national peut s'adresser à des experts qui connaissent bien le domaine et confronter leurs estimations. Il peut également les réunir pour qu'ils puissent échanger des arguments et parvenir à une estimation raisonnable.

En supposant que le résultat des discussions est une estimation de 10 de la formation brute de capital fixe des compagnies aériennes en voitures, le tableau suivant donne la meilleure estimation possible :

	Voitures	Camions	Avions	Total
Taxis Transporteurs routiers Compagnies aériennes	1990 0 10	0 2000 0	0 0 1000	1990 2000 1010
Total	2000	2000	1000	5000

Le problème pour le comptable national est maintenant de savoir s'il peut publier ce tableau. De son point de vue, il donne la meilleure information possible. Mais il faut savoir que lorsque les comptables nationaux publient leurs comptes, les utilisateurs s'attendent à ce que tous les chiffres publiés soient fiables et même, pour beaucoup, qu'ils soient parfaitement exacts.

Or, dans notre exemple, la formation brute de capital fixe en voitures des compagnies aériennes peut être aussi bien 15 que 5. Cette imprécision est acceptable pour le comptable national qui se place avant tout dans une perspective macroéconomique, elle est insupportable pour celui qui s'intéresse à ce chiffre en particulier, par exemple, s'il s'agit d'un concessionnaire automobile qui vend des voitures aux compagnies aériennes et qui cherche à évaluer sa part de marché.

Il donc important de comprendre que lorsque les comptables nationaux font leurs estimations, ils sont parfois amenés à transformer de l'information qualitative en information quantitative. Dans notre exemple, c'est davantage la perception qu'ont les experts de leur domaine que des données chiffrées qui a servi de base à l'estimation.

Ces estimations ont une précision faible mais elles permettent d'améliorer la qualité des comptes en multipliant les possibilités de recoupement de l'information. Il serait cependant dangereux de les utiliser à d'autres fins que la comptabilité nationale. Les comptables nationaux ne publient donc généralement leurs comptes qu'à un niveau d'agrégation supérieur à celui qu'ils utilisent, même s'ils doivent résister pour cela à la pression des utilisateurs qui demandent toujours davantage de détails.

L'évolution du travail des comptables nationaux

Même si l’avenir est par nature incertain, une évolution défavorable de l’environnement se dessine pour les comptes nationaux, notamment du fait de deux tendances lourdes qui devraient perdurer au cours des prochaines années :

• le relèvement du niveau des exigences imposées d'une part par les normes internationales, d'autre part par l’Union européenne et les pouvoirs publics ;
• la dégradation de la qualité des sources d’information sous la double pression de la mondialisation et d’un environnement réglementaire visant à alléger la charge statistique pesant sur les entreprises.

Les exigences imposées par l’Union européenne et les pouvoirs publics

L’Union européenne exerce une triple pression sur les services de comptabilité nationale :

• exigence en termes de résultats : toujours plus rapidement, toujours plus détaillés ;
• exigence en termes de méthodes : les méthodes évoluent, d’une part pour permettre une meilleure application des règlements européens en matière de déficit et de dette publics, d’autre part pour assurer un meilleur suivi de domaines considérés comme stratégiques, notamment la finance et l’économie de la connaissance. Ce mouvement initié à l’occasion de la mise en place du SEC 2010 est appelé à se poursuivre au cours des prochaines années ;
• exigence en termes de transparence : Eurostat et la Cour des comptes européenne veulent contrôler non seulement les résultats des comptes nationaux, mais aussi leur processus de production, ce qui se concrétise notamment par l’obligation de mettre en place des systèmes de supervision et de contrôle au sein des services de comptabilité nationale.

Parallèlement, sous la pression de l’opinion publique, les pouvoirs politiques sont incités à demander aux comptables nationaux d’aller vers une meilleure prise en compte des questions sociales, environnementales et régionales.

La dégradation de la qualité des sources d’information

Ces nouvelles exigences apparaissent alors que, dans le même temps, la qualité des sources d’information se dégrade.

En effet, la mondialisation rend plus difficile le suivi de l’activité économique nationale par les services statistiques suite à deux phénomènes :

• une part de plus en plus importante des flux de biens et services et des flux financiers se déroule en dehors des frontières nationales ;
• le morcellement des processus de production entre les pays se traduit par une instabilité des structures économiques qui remet en cause les procédures traditionnelles de validation des données.

En réponse à la mondialisation qui accentue la concurrence internationale, les États sont amenés à alléger le plus possible les contraintes pesant sur leurs entreprises. Au niveau européen, cela se traduit par une évolution de la règlementation visant à atténuer le poids de la charge statistique pesant sur les entreprises.

Cet allègement de la charge statistique pour les entreprises peut aller de pair avec un allègement du travail de collecte pour les services statistiques, mais il se traduit surtout par une dégradation sensible de la qualité de l’information.

Les services devant publier des statistiques exhaustives sont donc contraints de compenser cette dégradation par davantage d’hypothèses et davantage d’analyses. On peut alors anticiper une légère réduction des travaux automatisés pour les services statistiques mais un fort accroissement des travaux d’analyse nécessitant du personnel de haut niveau pour les comptables nationaux.

Une pression dangereuse

La politique économique européenne s’appuie de plus en plus sur la comptabilité nationale :

• les critères de déficit et de dette publics excessifs sont déterminés par rapport au PIB ;
• la ventilation des ressources propres de l’Union entre les États est faite à partir du revenu national brut (RNB), agrégat qui dérive du PIB ;
• l’affectation des fonds régionaux est décidée sur base des PIB régionaux.

Il devient dès lors indispensable que les comptes nationaux soient parfaitement fiables et reposent sur des données objectivement mesurables et vérifiables.

Le problème est que, comme nous venons de le voir, pour élaborer leurs comptes, les comptables nationaux se trouvent confrontés à un double problème :

• d’une part, ils ne disposent pas, et ne disposeront jamais, de toute l'information nécessaire à la réalisation de comptes économiques complets ;
• d’autre part, la cohérence du cadre comptable fait apparaître que les statistiques disponibles sont généralement incompatibles entre elles.

Si la comptabilité nationale existe, c’est parce que les comptables nationaux considèrent :

• d’une part, que malgré leurs insuffisances, les statistiques disponibles permettent déjà de dégager une bonne vision de la réalité économique, si bien qu’il est préférable de les compléter par des estimations, même approximatives, plutôt que de renoncer à les utiliser ;
• d’autre part, que la confrontation des sources et leur arbitrage dans un cadre cohérent permet de les améliorer.

Malheureusement, pour réaliser leurs estimations et leurs arbitrages, les comptables nationaux doivent nécessairement s’appuyer sur leur jugement, c’est-à-dire sur un élément subjectif qui peut être remis en cause lors des opérations de contrôle.

En conséquence, des contrôles exigeant une justification rigoureuse et objective de toutes les évaluations retenues par les comptables nationaux pourraient inciter ces derniers à se couvrir en éliminant le problème de l’incohérence des sources, c'est-à-dire en adoptant sans les modifier quelques-unes d’entre elles et en calculant par solde les postes correspondant aux données les moins fiables, ce qui peut paraître la démarche la plus rigoureuse pour les vérificateurs.

En réalité, cela affaiblirait les comptes nationaux car aucune statistique n’est parfaitement fiable et que l’un des principaux intérêts de la comptabilité nationale est précisément d’organiser la confrontation des sources.

Ce problème devrait s'aggraver à l'avenir avec la détérioration prévisible des sources d'information et donc le recours de plus en plus important aux estimations et aux arbitrages.

Au niveau européen, le contrôle de la qualité des comptes nationaux est réalisé principalement par Eurostat et la Cour des comptes européenne. Si l'on peut considérer que ces contrôles ont eu jusqu'ici davantage un effet positif que négatif sur la qualité des comptes, c'est d'une part parce que le contrôle des comptes nationaux d'un pays par Eurostat est fait en coopération avec les comptables nationaux des autres pays de l'Union, d'autre part parce que la Cour des comptes européenne agit en concertation avec Eurostat.

Il n'en reste pas moins qu'il est difficile pour des personnes venant de domaines extérieurs à la comptabilité nationale de comprendre – et d'accepter –  que les comptes nationaux comportent nécessairement une part de subjectivité, si bien que leur qualité dépend au moins autant de la qualité des équipes en charge de les élaborer que de la qualité des données de base.

Les comptables nationaux sont donc condamnés à toujours faire un effort de pédagogie pour faire comprendre aux utilisateurs quelle est la réalité de leur métier, faute de quoi ils risqueraient d'être contraints d'adopter des méthodes incompatibles avec l'élaboration de comptes nationaux de qualité.

Auteur : Francis Malherbe

• Version PDF