L'approche multidimensionnelle dans les bases de données

Les bases de données relationnelles

L'approche multidimensionnelle permet de traiter simplement des questions qui mettent en jeu de grandes masses de données. Nous considérerons ici qu'une base de données relationnelles est constituée d'un ensemble de tables, chaque table pouvant être décrite sous la forme d'un tableau où les colonnes correspondent à des variables et les lignes à des enregistrements.

Par exemple, le tableau ci-dessous donne la valeur des variables P1, P2 et B1 de plusieurs secteurs d'activité AE.

AE	P1	P2	B1
B01	800	300	500
B02	500	400	100
B02	600	450	150
B03	200	50	150
B04	700	400	300
B04	900	500	400

La première ligne du tableau donne le nom des différentes variables, les autres lignes correspondent aux enregistrements. Dans une même table, le nombre d'enregistrements est indifférent mais chaque enregistrement doit avoir la même structure, c'est-à-dire comporter les mêmes variables et dans le même ordre. Ainsi, si l'on ajoutait un nouvel enregistrement à cette table, il devrait impérativement comprendre les variables AE, P1, P2 et B1 dans cet ordre.

Nous pouvons considérer que le tableau décrit une économie en l'étudiant sous deux critères différents : les opérations de la comptabilité nationale et les activités économiques. Nous remarquons alors que les deux critères ne sont pas traités de manière symétrique dans la table de notre base de données relationnelle. En effet, on ne peut pas ajouter de nouvelles opérations à la table sans porter atteinte à sa structure alors qu'on peut ajouter autant de nouvelles activités que l'on désire.

Or, il est souvent intéressant de traiter les critères de manière symétrique, surtout si l'on souhaite travailler avec plus de deux critères. Nous allons donc présenter la table de manière différente mais en conservant les mêmes informations et en respectant la symétrie de traitement des critères. Pour cela, nous allons créer une table où chaque valeur du tableau apparaîtra avec les modalités des deux critères dans un même enregistrement, le nombre d'enregistrements étant alors égal au nombre de valeurs du tableau initial. La nouvelle table sera constituée de trois variables, une variable pour chaque critère et une variable pour la valeur. Elle pourra se présenter de la manière suivante :

AE	OP	VAL
B01	P1	800
B02	P1	500
B02	P1	600
B03	P1	200
B04	P1	700
B04	P1	900
B01	P2	300
B02	P2	400
B02	P2	450
B03	P2	50
B04	P2	400
B04	P2	500
B01	B1	500
B02	B1	100
B02	B1	150
B03	B1	150
B04	B1	300
B04	B1	400

On constate que, par rapport à l'ancienne, la nouvelle table est plus volumineuse, mais, en contrepartie, elle présente l'avantage certain d'être plus facilement modifiable puisque l'on peut, sans porter atteinte à sa structure, ajouter autant de nouvelles opérations que l'on désire.

L'autre grand avantage de ce type de tables est qu'il est très facile de travailler avec plus de deux critères. Par exemple, si nous souhaitons introduire également l'année, il est possible de décrire simplement l'ensemble des données avec une table à 4 colonnes comme celle qui est présentée ci-dessous :

AE	DA	OP	VAL
B01	2004	P1	800
B02	2004	P1	500
B02	2005	P1	600
B03	2004	P1	200
B04	2004	P1	700
B04	2005	P1	900
B01	2004	P2	300
B02	2004	P2	400
B02	2005	P2	450
B03	2004	P2	50
B04	2004	P2	400
B04	2005	P2	500
B01	2004	B1	500
B02	2004	B1	100
B02	2005	B1	150
B03	2004	B1	150
B04	2004	B1	300
B04	2005	B1	400

Cette simplicité de travail avec plusieurs critères est fondamentale pour le comptable national. Déjà, il est facile de voir qu'avec trois critères il aurait été difficile de travailler avec une table du type de la première table présentée car il aurait été nécessaire de multiplier le nombre de colonnes par le nombre d'années. En pratique, travailler avec une table présentant en colonnes toutes les années et toutes les opérations soulèverait deux problèmes, le premier est qu'il est difficile de travailler avec de nombreuses variables, le second est qu'il faudrait modifier la structure du tableau chaque fois que l'on voudrait ajouter une année. Or, le comptable national travaille habituellement avec plus de trois critères. Il utilise, par exemple, l'année, le secteur institutionnel, le secteur d'activité, la branche, le produit, l'opération, le critère ressources/emplois et la source des données. Il est donc pratiquement impossible de travailler avec des tableaux analogues au premier tableau présenté.

Les critères prennent le nom de dimensions et les bases de données où les tables sont structurées de cette manière peuvent être qualifiées de bases de données multidimensionnelles et les tables d'hypercubes.

Les hiérarchies

Les bases de données organisées selon une approche multidimensionnelle sont extrêmement performantes. Elles permettent, en effet, de réaliser très simplement un certain nombre de traitements. Parmi eux, l'un des plus intéressants est l'introduction de hiérarchies. Ainsi, dans notre exemple, nous avons introduit 4 activités différentes correspondant à un niveau de la nomenclature d'activités que nous appellerons le niveau G. Ces secteurs B01, B02, B03, B04 sont regroupés au niveau supérieur, appelé niveau F, en deux secteurs et B1 (qui regroupe B01 et B02) et B2 (qui regroupe B03 et B04). Au niveau supérieur, appelé niveau E, les deux secteurs B1 et B2 sont regroupés en un seul, le secteur B. Nous avons ici l'exemple d'une hiérarchie sur les secteurs d'activité, l'activité B a deux fils B1 et B2, le secteur B1 a lui-même deux fils B01 et B02, le secteur B2 ayant B03 et B04 pour fils.

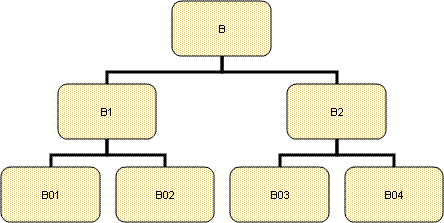
On peut souhaiter obtenir les résultats non seulement au niveau G mais également aux niveaux supérieurs. Nous pourrons y parvenir et passer d'un niveau de nomenclature à l'autre en introduisant une table de passage. Il y a deux manières possibles de procéder pour cela, on peut souhaiter disposer de chaque niveau de nomenclature dans deux dimensions séparées ou l'on peut préférer disposer des deux niveaux dans la même dimension.

Dans le premier cas, on fera appel à une table passage du type suivant :

AEG	AEF	AEE
B01	B1	B
B02	B1	B
B03	B2	B
B04	B2	B

Si nous appelons PROD la table de données et HAE la table de passage, la requête suivante nous permet de calculer les données, par exemple, au niveau F :

SELECT H.AEF, P.OP, sum(P.VAL) as VAL
FROM PROD P, HAE H
WHERE P.AE=H.AEG
GROUP BY H.AEF, P.OP
;

Nous obtenons :

AEF	OP	VAL
B1	P1	1900
B2	P1	1800
B1	P2	1150
B2	P2	950
B1	B1	750
B2	B1	850

Nous aurions également pu calculer le niveau E de la même manière en remplaçant dans la requête précédente GROUP BY H.AEF par GROUP BY H.AEE.

Si nous souhaitons faire apparaître dans une même dimension tous les niveaux de la hiérarchie nous devons utiliser la table suivante qui montre les différents niveaux hiérarchiques pour chaque élément du niveau le plus bas :

AEG	AE
B01	B01
B02	B02
B03	B03
B04	B04
B01	B1
B02	B1
B03	B2
B04	B2
B01	B
B02	B
B03	B
B04	B

En utilisant la requête suivante :

SELECT H.AE, P.OP, sum(P.VAL) as VAL
FROM PROD P, HAE H
WHERE P.AE=H.AEG
GROUP BY H.AE, P.OP
;

Nous obtenons :

AE	OP	VAL
B01	P1	800
B02	P1	1100
B03	P1	200
B04	P1	1600
B01	P2	300
B02	P2	850
B03	P2	50
B04	P2	900
B01	B1	500
B02	B1	250
B03	B1	150
B04	B1	700
B1	P1	1900
B2	P1	1800
B1	P2	1150
B2	P2	950
B1	B1	750
B2	B1	850
B	P1	3700
B	P2	2100
B	B1	1600

Les combinaisons de modalités

Il est souvent utile pour le comptable national de calculer des combinaisons d'un certain nombre de modalités d'une ou de plusieurs dimensions.

Supposons, par exemple, que nous cherchions à vérifier le calcul de B1 (la valeur ajoutée) en faisant la différence entre P1 (la production) et P2 (la consommation intermédiaire). Il suffit pour cela d'introduire une table de passage qui montre comment passer des opérations P1 et P2 à une nouvelle opération B1C. Cette table de passage se présentera alors ainsi :

OPC	OP	VAL
B1C	P1	1
B1C	P2	-1

Si nous appelons PROD la table de données et CALC la table de passage, la requête suivante nous permet de calculer les données :

SELECT P.AE, C.OPC, sum(P.VAL*C.VAL) as VAL
FROM PROD P, CALC C
WHERE P.OP=C.OP
GROUP BY P.AE, C.OPC
;

Nous obtenons :

AE	OP	VAL
B01	B1C	500
B02	B1C	250
B03	B1C	150
B04	B1C	700

Cette manière de travailler est extrêmement utile pour le contrôle et la maintenance du processus d'élaboration des comptes nationaux. En effet, avec cette approche il est possible de séparer les trois éléments fondamentaux du processus :

• Les données
• Les règles de calcul
• La programmation

Les données et les règles de calcul correspondent, en effet, à deux tables différentes qu'il est possible de modifier et de vérifier séparément, la programmation se réduisant à des requêtes SQL très simples faciles à contrôler.

Les tables de passage

Les programmes qui permettent de passer des données des comptes des entreprises aux estimations de la comptabilité nationale font largement appel aux hypercubes. Ceux-ci peuvent être traités par des logiciels spécialisés mais ils peuvent également être traités dans le cadre de bases de données relationnelles par le langage SQL.

Supposons que l'économie soit constituée de 4 sous-secteurs d'activité AEGA01, AEGA02, AEGB01, AEGB02 et que nous cherchions à calculer les opérations de la comptabilité nationale P1, P2 et B1 à partir des variables suivantes portant sur les statistiques d'entreprises :

R212 Achats matières premières
POURBOIR Pourboires
RC302 Production vendue
TRANSPRO Transport sur production

Les formules de calcul étant les suivantes :

P1 = RC302 + POURBOIR - TRANSPRO
P2 = R212 -TRANSPRO
B1 = P1 - P2

La première étape consiste à traduire ces égalités dans le cadre d'une matrice, c'est-à-dire d'un hypercube à deux dimensions, de la manière suivante :

		PCRP	PCEA	PCEA
		P1	P2	B1
Achats matières premières	R212		1	-1
Pourboires	POURBOIR	1		1
Production vendue	RC302	1		1
Transport sur production	TRANSPRO	-1	-1	0

Ce tableau montre comment passer des statistiques d'entreprises à la comptabilité nationale. Les valeurs 1 et -1 indiquent les coefficients à appliquer aux données d'entreprise pour passer à l'opération de la comptabilité nationale. Par exemple, P1 est calculé en faisant la somme suivante :

POURBOIR affecté du coefficient 1
RC302 affecté du coefficient 1
TRANSPRO affecté du coefficient -1

Les dimensions de ce tableau sont :

• l'opération de comptabilité nationale que nous désignerons par le code OP
• les éléments de calcul que nous appellerons variables exogènes et que nous considérerons appartenir à une dimension EX

Ce tableau possède même une troisième dimension : la dimension PC qui permet de déterminer si l'opération de comptabilité nationale correspond à une ressource ou à un emploi.

Le grand intérêt de ce tableau est de permettre une double lecture :

• en colonne, il montre comment est calculée une opération ;
• en ligne, il montre quel est l'impact d'une variable exogène sur les différentes opérations et en particulier les soldes tels que B1.

Ce tableau peut être représenté par un hypercube à trois dimensions. Dans une base de données relationnelle, un hypercube correspond à une table, c'est-à-dire à un tableau où les colonnes correspondent aux variables et les lignes aux enregistrements, structurée de la manière suivante :

• Un hypercube ne comporte qu'une seule variable numérique, les autres sont des variables alphanumériques correspondant à des critères, c'est-à-dire aux dimensions du cube.

Ainsi, dans notre exemple, notre table de passage se présentera de la manière suivante :

OP	PC	EX	VAL
P2	PCEA	R212	1
B1	PCEA	R212	-1
P1	PCRP	POURBOIR	1
B1	PCEA	POURBOIR	1
P1	PCRP	RC302	1
B1	PCEA	RC302	1
P1	PCRP	TRANSPRO	-1
P2	PCEA	TRANSPRO	-1

Il ne reste plus qu'à présenter les variables exogènes sous la forme d'un hypercube. Celui-ci possèdera les dimensions suivantes :

• DA : l'année
• SI : le secteur institutionnel
• AE : le sous-secteur d'activité
• EX : la variable exogène

Supposons que les données exogènes se présentent sous la forme d'un hypercube à quatre dimensions, l'année (DA), le secteur institutionnel (SI), l'activité économique (AE) et le type de variable exogène (EX). Par exemple, cet hypercube se présente de la manière suivante :

DA	SI	AE	EX	VAL
DA2000	SIS11	AEGA01	RC302	200
DA2000	SIS11	AEGA02	RC302	300
DA2000	SIS11	AEGB01	RC302	400
DA2000	SIS11	AEGB02	RC302	500
DA2000	SIS11	AEGA01	R212	100
DA2000	SIS11	AEGA02	R212	150
DA2000	SIS11	AEGB01	R212	200
DA2000	SIS11	AEGB02	R212	250
DA2000	SIS11	AEGB01	POURBOIR	10
DA2000	SIS11	AEGB02	POURBOIR	20
DA2000	SIS11	AEGA01	TRANSPRO	10
DA2000	SIS11	AEGA02	TRANSPRO	30
DA2000	SIS11	AEGB01	TRANSPRO	20
DA2000	SIS11	AEGB02	TRANSPRO	30
DA2000	SIS14AA	AEGA01	RC302	100
DA2000	SIS14AA	AEGA02	RC302	150
DA2000	SIS14AA	AEGB01	RC302	200
DA2000	SIS14AA	AEGB02	RC302	250
DA2000	SIS14AA	AEGA01	R212	50
DA2000	SIS14AA	AEGA02	R212	75
DA2000	SIS14AA	AEGB01	R212	100
DA2000	SIS14AA	AEGB02	R212	125
DA2000	SIS14AA	AEGA01	POURBOIR	0
DA2000	SIS14AA	AEGA02	POURBOIR	0
DA2000	SIS14AA	AEGB01	POURBOIR	5
DA2000	SIS14AA	AEGB02	POURBOIR	10
DA2000	SIS14AA	AEGA01	TRANSPRO	5
DA2000	SIS14AA	AEGA02	TRANSPRO	15
DA2000	SIS14AA	AEGB01	TRANSPRO	10
DA2000	SIS14AA	AEGB02	TRANSPRO	15

Le programme de passage aux comptes est alors extrêmement simple : il consiste à réaliser à l'aide d'une requête SQL une jointure multipliant les deux hypercubes l'un par l'autre.

Si nous appelons TablePac l'hypercube correspondant à la table de passage et Exo l'hypercube des variables exogènes, la requête s'écrit de la manière suivante :

SELECT e.DA, e.SI, e.AE, e.EX, t.OP, t.PC, e.VAL*t.VAL as VAL
FROM TablePac t, Exo e
WHERE t.EX=e.EX

Les résultats de cette requête peuvent eux-mêmes être stockés dans une table qui comprend tous les résultats et qui montre comment ces résultats ont été obtenus. Par exemple, cette table peut être lue par un tableau croisé dynamique d'Excel qui présente l'avantage de pouvoir présenter facilement différents tableaux à partir de la même table de données. Ainsi, nous pouvons faire apparaître un premier tableau croisant les opérations, les secteurs institutionnels et les activités économiques :

OP	SI	A01	A02	B01	B02	Total
B1	SIS11	100	150	210	270	730
	SIS14AA	50	75	105	135	365
Somme B1		150	225	315	405	1 095
P1	SIS11	190	270	390	490	1 340
	SIS14AA	95	135	195	245	670
Somme P1		285	405	585	735	2 010
P2	SIS11	90	120	180	220	610
	SIS14AA	45	60	90	110	305
Somme P2		135	180	270	330	915

Mais il peut également être intéressant de montrer comment sont calculées les opérations à partir des variables exogènes. Ainsi le tableau suivant met en évidence le calcul de la production :

EX	A01	A02	B01	B02	Total
POURBOIR	0	0	15	30	45
RC302	300	450	600	750	2 100
TRANSPRO	-15	-45	-30	-45	-135
Total	285	405	585	735	2 010

 

Si on avait voulu uniquement les opérations de la comptabilité nationale, on aurait pu utiliser la requête ci-dessous :

SELECT e.DA, e.SI, e.AE, t.OP, t.PC, sum(e.VAL*t.VAL) as VAL
FROM TablePac t, Exo e
WHERE t.EX=e.EX
GROUP BY e.DA, e.SI, e.AE, t.OP, t.PC

On aurait obtenu :

DA	SI	AE	OP	PC	VAL
DA2000	SIS11	AEGA01	B1	PCEA	100
DA2000	SIS11	AEGA01	P1	PCRP	190
DA2000	SIS11	AEGA01	P2	PCEA	90
DA2000	SIS11	AEGA02	B1	PCEA	150
DA2000	SIS11	AEGA02	P1	PCRP	270
DA2000	SIS11	AEGA02	P2	PCEA	120
DA2000	SIS11	AEGB01	B1	PCEA	210
DA2000	SIS11	AEGB01	P1	PCRP	390
DA2000	SIS11	AEGB01	P2	PCEA	180
DA2000	SIS11	AEGB02	B1	PCEA	270
DA2000	SIS11	AEGB02	P1	PCRP	490
DA2000	SIS11	AEGB02	P2	PCEA	220
DA2000	SIS14AA	AEGA01	B1	PCEA	50
DA2000	SIS14AA	AEGA01	P1	PCRP	95
DA2000	SIS14AA	AEGA01	P2	PCEA	45
DA2000	SIS14AA	AEGA02	B1	PCEA	75
DA2000	SIS14AA	AEGA02	P1	PCRP	135
DA2000	SIS14AA	AEGA02	P2	PCEA	60
DA2000	SIS14AA	AEGB01	B1	PCEA	105
DA2000	SIS14AA	AEGB01	P1	PCRP	195
DA2000	SIS14AA	AEGB01	P2	PCEA	90
DA2000	SIS14AA	AEGB02	B1	PCEA	135
DA2000	SIS14AA	AEGB02	P1	PCRP	245
DA2000	SIS14AA	AEGB02	P2	PCEA	110

Les ventilations

La ventilation est une opération qui consiste à répartir une donnée globale en ses différents éléments à partir d'une structure. Par exemple, considérons trois activités : l'agriculture, l'industrie et les services et supposons que nous connaissions la valeur ajoutée totale de ces trois activités mais pas la valeur ajoutée de chaque activité. Supposons également que nous connaissions le nombre de salariés dans chaque activité. Nous pouvons obtenir une première estimation de la valeur ajoutée par activité en répartissant la valeur ajoutée globale proportionnellement au nombre de salariés de chaque activité.

Par exemple :

• Valeur ajoutée globale : 3000
• Nombre de salariés
  • Agriculture : 200
  • Industrie : 500
  • Services : 300

Pour calculer la valeur ajoutée d'une activité, on peut procéder de deux manières différentes. La première consiste à calculer des coefficients représentatifs de la structure et à les appliquer à la valeur ajoutée totale. Par exemple, le nombre total de salariés est 1000, on peut calculer pour l'agriculture un coefficient de structure égal à 200/1000=20% et l'appliquer à la valeur ajoutée totale, on obtient pour l'agriculture une valeur ajoutée égale à 3000×20%=600.

La deuxième manière consiste à considérer que faire une ventilation c’est appliquer une homothétie à la structure, c’est-à-dire multiplier tous ses éléments par un même coefficient, ce coefficient étant égal au rapport entre le total que l’on veut atteindre, c’est-à-dire la donnée à ventiler, et le total correspondant de la structure.

Ainsi, dans notre exemple, le nombre total de salariés est égal à 1000, pour calculer la valeur ajoutée pour chaque activité, il suffit de multiplier le nombre de salariés par 3000/1000=3. On a, en quelque sorte, "dilaté" la structure pour l'amener au bon total.

L'intérêt d'utiliser des hypercubes pour faire des ventilations est que l'on peut en faire un grand nombre en une seule fois.

Par exemple, supposons que nous voulions ventiler la valeur ajoutée de deux branches BR1 et BR2 par produit en connaissant la valeur ajoutée totale de chaque branche :

BR1	BR2
2000	1000

et la structure par produit :

	BR1	BR2
PR1	30	50
PR2	50	50
PR3	20	150

Commençons par créer deux tables correspondant à des hypercubes :

Aventiler

BR	VAL
BR1	2000
BR2	1000

Structure

BR	PR	VAL
BR1	PR1	30
BR1	PR2	50
BR1	PR3	20
BR2	PR1	50
BR2	PR2	50
BR2	PR3	150

On se propose d'appliquer ici la deuxième méthode de ventilation. On commence par calculer dans la structure les totaux des produits pour les deux branches et on les stocke dans la table Total. Pour cela, on utilise la requête suivante :

INSERT INTO Total
SELECT s.BR, sum(s.VAL) as VAL
FROM Structure s
GROUP BY s.BR
;

On obtient le résultat suivant :

Total

BR	VAL
BR1	100
BR2	250

On peut ensuite calculer les coefficients multiplicateurs en "divisant" la table Aventiler par la table Total. Pour cela on utilise la requête suivante qui stocke les coefficients dans la table Coef :

INSERT INTO Coef
SELECT a.BR, a.VAL/t.VAL as VAL
FROM Aventiler a, Total t
WHERE a.BR=t.BR
;

On obtient :

Coef

BR	VAL
BR1	20
BR2	4

Il aurait été possible de réaliser les deux étapes précédentes en une seule, sans créer la table Total, en utilisant à sa place la requête qui la crée comme une sous-requête :

INSERT INTO Coef
SELECT a.BR, a.VAL/t.VAL as VAL
FROM Aventiler a,
    (
    SELECT s.BR, sum(s.VAL) as VAL
    FROM Structure s
    GROUP BY s.BR
    ) t
WHERE a.BR=t.BR
;

On peut maintenant multiplier les coefficients multiplicateurs par la structure et les stocker dans la table Ventilés grâce à la requête suivante  :

INSERT INTO Ventilés
SELECT s.BR, s.PR, (c.VAL*s.VAL) as VAL
FROM Coef c, Structure s
WHERE c.BR=s.BR
;

On obtient :

Ventilés

BR	PR	VAL
BR1	PR3	400
BR1	PR2	1000
BR1	PR1	600
BR2	PR3	600
BR2	PR2	200
BR2	PR1	200

Il aurait été possible de faire l'ensemble de la procédure en une seule requête en remplaçant la table Coef par la requête qui lui a donné naissance :

INSERT INTO Ventilés
SELECT s.BR, s.PR, (c.VAL*s.VAL) as VAL
FROM Structure s,
    (
    SELECT a.BR, a.VAL/t.VAL as VAL
    FROM Aventiler a,
        (
        SELECT s.BR, sum(s.VAL) as VAL
        FROM Structure s
        GROUP BY s.BR
        ) t
    WHERE a.BR=t.BR
    ) c
WHERE c.BR=s.BR
;

Il est souvent plus prudent de commencer par procéder en plusieurs étapes avant d'écrire une seule requête composée de plusieurs sous-requêtes.

Ventilation avec plusieurs éléments fixés

Dans certains cas, certains éléments de la ventilation sont déjà connus. Par exemple, supposons que dans la ventilation précédente, les éléments suivants soient déjà connus :

	BR1	BR2
PR1		100
PR2	50

Il faut alors procéder de la manière suivante :

• éliminer de la structure les éléments correspondants à ceux déjà connus ;
• déduire du total à ventiler les éléments déjà connus ;
• faire la ventilation avec la nouvelle structure et les nouveaux totaux à ventiler ;
• ajouter les éléments déjà connus.

Commençons par créer une table hypercube correspondant aux données connues :

DéjàVentilé

BR	PR	VAL
BR1	PR2	50
BR2	PR1	100

Créons la table Mstructure correspondant à la nouvelle structure grâce à la requête suivante :

INSERT INTO Mstructure
SELECT * FROM Structure s
WHERE NOT EXISTS
(SELECT * FROM DéjàVentilé d
WHERE d.BR=s.BR AND d.PR=s.PR)

Dans cette requête on a utilisé la clause NOT EXISTS pour éliminer les enregistrements communs aux deux tables Structure et DéjàVentilé. On obtient :

Mstructure

BR	PR	VAL
BR1	PR1	30
BR1	PR3	20
BR2	PR2	50
BR2	PR3	150

Les valeurs déjà ventilées doivent être déduites des valeurs à ventiler, pour cela elles peuvent être regroupées dans la table Màventiler grâce à la requête SQL suivante :

INSERT INTO MàVentiler
SELECT u.BR, sum(u.VAL) as VAL
FROM
    (
    SELECT BR, VAL
    FROM
    Aventiler
    UNION ALL
    SELECT d.BR, sum(-d.VAL) as VAL
    FROM DéjàVentilé d
    GROUP BY d.BR
    ) u
GROUP BY u.BR
;

Cette requête utilise la commande UNION ALL pour réunir deux tables. La première table est Aventiler, la seconde est la somme par branche des valeurs déjà ventilées avec un signe négatif. Dans la table obtenue on fait alors le total par branche des enregistrements.

Notons que dans Access on ne peut pas associer directement UNION ALL et INSERT INTO, si bien que l'on est obligé d'utiliser une sous-requête pour procéder avec une seule requête.

Nous obtenons :

MàVentiler

BR	VAL
BR1	1950
BR2	900

On peut maintenant, comme dans le cas d'une ventilation simple, créer la table Coef des coefficients multiplicateurs en "divisant" la table MàVentiler par le total par branche de la table Mstructure. On peut utiliser pour cela la requête suivante :

INSERT INTO Coef
SELECT a.BR, a.VAL/t.VAL as VAL
FROM Màventiler a,
    (
    SELECT s.BR, sum(s.VAL) as VAL
    FROM Mstructure s
    GROUP BY s.BR
    ) t
WHERE a.BR=t.BR
;

On obtient :

Coef

BR	VAL
BR1	39
BR2	4,5

On "multiplie" maintenant la table Mstructure par la table Coef et on insère le résultat dans la table Ventilés grâce à la requête suivante :

INSERT INTO Ventilés
SELECT s.BR, s.PR, (c.VAL*s.VAL) as VAL
FROM Coef c, Mstructure s
WHERE c.BR=s.BR
;

On obtient :

Ventilés

BR	PR	VAL
BR1	PR3	780
BR1	PR1	1170
BR2	PR3	675
BR2	PR2	225

Il ne reste plus qu'à insérer dans la table Ventilés les éléments déjà ventilés graâce à la requête :

INSERT INTO Ventilés
SELECT *
FROM DéjàVentilé
;

On obtient :

Ventilés

BR	PR	VAL
BR1	PR3	780
BR1	PR1	1170
BR2	PR3	675
BR2	PR2	225
BR1	PR2	50
BR2	PR1	100

On peut, là encore, réduire le nombre de tables en en remplaçant certaines par des sous-requêtes. Par exemple, les deux dernières requêtes peuvent être remplacées par la suivante :

INSERT INTO Ventilés
SELECT *
FROM
     (
    SELECT s.BR, s.PR, (c.VAL*s.VAL) as VAL
     FROM Coef c, Mstructure s
     WHERE c.BR=s.BR
    UNION ALL
     SELECT *
     FROM DéjàVentilé
    )
;

Les produits matriciels

Il est possible de réaliser des produits de matrices de très grandes dimensions avec des requêtes SQL. En effet, on peut considérer une matrice comme un hypercube à deux dimensions, si bien que faire un produit matriciel revient à faire des jointures par des requêtes SQL comme nous pouvons le montrer à partir d'un exemple simple.

Supposons donc une économie constituée de deux secteurs et de trois branches, nous disposons d'une matrice de passage secteurs-branches que nous nommons "Structure" et d'une matrice de production par secteurs "Secteurs". La matrice de passage secteurs-branches montre la répartition de la production de chaque secteur par activité économique et elle permet de calculer la production par branche lorsque l'on connaît la production par secteur. Ainsi, la matrice de production par branche s'obtient en faisant le produit de la matrice Structure par la matrice Secteurs. Par exemple :

Structure   S1 S2 B1 0,5 0,3 B2 0,2 0,6 B3 0,3 0,1

Secteurs     Prod   S1   100 S2   200

Branches     Prod   B1   110 B2   140 B3   50

Que fait le produit matriciel ?

• il crée une nouvelle matrice ayant autant de lignes que la première matrice et de colonnes que la seconde. Dans notre exemple, il crée une matrice de trois lignes correspondant aux trois branches et une colonne correspondant à la valeur de la production.
• pour calculer un élément se situant dans la matrice résultat à la ligne i et à la colonne j, il associe tous les éléments de la ligne i de la première matrice à tous les éléments de la colonne j de la deuxième matrice. Pour que cela soit possible, il est nécessaire que le nombre de colonnes de la première matrice soit égal au nombre de lignes de la deuxième. Dans notre exemple, cette condition est vérifiée parce que les lignes de la première matrice et les colonnes de la seconde correspondent toutes deux aux modalités du même critère, le secteur.
• l'association est faite dans l'ordre, c'est-à-dire qu'à chaque secteur de la première matrice est associé le même secteur de la deuxième matrice.
• le calcul consiste à multiplier les éléments correspondants et à faire la somme des résultats.

Il est facile de reproduire ce processus avec une requête SQL, à condition ,toutefois, d'avoir structuré les données en hypercubes. Ainsi, nous aurions pu saisir la même information en créant dans une base de données relationnelle une table Structure et une table Secteurs de la manière suivante :

Structure		Secteurs
Secteur Branche  Taux  S1 B1 0,5 S2 B1 0,3 S1 B2 0,2 S2 B2 0,6 S1 B3 0,3 S2 B3 0,1		Secteur  Prod  S1 100 S2 200

On peut réaliser une jointure des deux tables par une requête SQL qui va multiplier les valeurs de la première table par celles de la deuxième, sous la condition que l'association ne portera que sur des données correspondant au même secteur. Cette requête peut s'écrire ainsi :

SELECT Structure.Secteur, Branche, Taux*Prod as Valeur
FROM Structure, Secteurs
WHERE Structure.Secteur=Secteurs.Secteur
;

Cette requête fait le produit cartésien des deux ensembles que constituent les deux tables en ne retenant que les combinaisons où le secteur est commun. On obtient alors la table Branches suivant :

Branches

Secteur	Branche	Valeur
S1	B1	50
S2	B1	60
S1	B2	20
S2	B2	120
S1	B3	30
S2	B3	20

Cette table peut être lue directement par un tableau croisé dynamique qui donnera le résultat en ne sélectionnant que le critère Branche. On peut également générer directement la table résultat par la requête SQL suivante :

SELECT Branche, SUM(Taux*Prod) as Valeur
FROM Structure, Secteurs
WHERE Structure.Secteur=Secteurs.Secteur
GROUP BY Branche
;

Ce qui donne :

Branche	Valeur
B1	110
B2	140
B3	50

On peut ainsi faire des produits de matrices de grande taille, par exemple de 1000 x 1000.

Notons, pour finir que les requêtes SQL portant sur des hypercubes sont plus puissantes que les produits matriciels et qu'elles en constituent en quelque sorte une extension. Il est, en effet, possible de travailler avec plus de deux critères. On peut ainsi ajouter des critères de taille et de catégorie juridique et obtenir par la même requête ce qui nécessiterait le recours à une multitude de produits matriciels.

Auteur : Francis Malherbe

• Version PDF