Prix et volumes

Le volume

L'un des objectifs principaux de la comptabilité nationale est la mesure de la croissance de l'activité économique. Mais, pour réaliser cet objectif, elle se trouve confrontée à un problème majeur, toutes ses données sont exprimées en valeurs monétaires, c'est-à-dire mesurées à partir d'un étalon de mesure dont la valeur ne reste pas stable avec le temps.

Tous les pays ont connu suffisamment de périodes d'inflation pour savoir que la monnaie se déprécie parfois d'une manière dramatique. Si la monnaie n'est pas un bon étalon de valeur, comment mesurer la croissance ? C'est un problème qui a longtemps préoccupé les économistes et qui suscite encore de nos jours de nombreux débats car il s'agit d'un sujet particulièrement sensible.

S'il n'y avait qu'un produit, par exemple le blé, la situation serait relativement simple. Pour mesurer la croissance de la production, il suffirait de suivre l'évolution des quantités produites. Mais, malheureusement pour le comptable national, l'économie comporte plus d'un produit ! Supposons donc que l'économie produise non seulement du blé mais aussi du poisson. Il est, bien entendu, toujours possible de suivre les évolutions des quantités produites de blé et de poisson. Supposons donc que ces quantités évoluent de la manière présentée dans le tableau ci-dessous :

Quantités produites

	T1	T2	T3
Blé	200	240	200
Poisson	100	120	150

Évolution par rapport à la période précédente

	T1	T2	T3
Blé		20%	-17%
Poisson		20%	25%

Entre la période 1 et la période 2, les quantités de blé et de poisson évoluent toutes deux de 20%, il semble donc raisonnable de dire que la croissance de l'économie s'établit, elle aussi, à 20%. Mais, entre la période 2 et la période 3, les quantités de blé et de poisson évoluent différemment puisque les quantités de blé baissent de 17% alors que celles de poisson augmentent de 25%. Que dire de la croissance globale ? Il pourrait être tentant de considérer les quantités globales produites mais nous savons depuis l'école primaire qu'additionner des quantités de produits de nature différente n'a pas de sens.

Pour résoudre cette difficulté les comptables nationaux sont partis de l'équation de base dans le domaine des prix :

Cette égalité signifiant que la valeur monétaire (v) d'un produit est égale au produit de son prix (p) par sa quantité (q).

Lorsqu'il y a plusieurs produits, cette égalité devient :

V = Σ_i p_i . q_i

L'indice i désigne ici un produit donné. Pour différencier les périodes on peut également utiliser un exposant. Par exemple, la valeur à la période 1 s'écrit :

V¹ = Σ_i p_i¹ . q_i¹

Si, dans les comparaisons de valeurs entre deux périodes, on veut éliminer l'effet de l'inflation des évaluations de la comptabilité nationale, un moyen simple consiste à valoriser les quantités des deux périodes aux mêmes prix.

Par exemple, lorsque l'on cherche à comparer deux périodes successives, il est possible de valoriser les quantités de la deuxième période aux prix de la première période.

Les comptables nationaux introduisent donc la notion de volume qui peut être définie comme une valeur aux prix constants. Ainsi, le volume de la production de l'ensemble des produits à la deuxième période est égal à :

Vol² = Σ_i p_i¹ . q_i²

Ce volume peut être comparé à la valeur de l'ensemble des produits à la période 1 aux prix courants, c'est-à-dire aux prix de cette même période 1, puisque ces deux grandeurs sont évaluées en utilisant toutes deux les prix de la même période.

Val¹ = Σ_i p_i¹ . q_i¹

Supposons, par exemple, que les prix aux trois périodes soient les suivants :

Prix des produits

	T1	T2	T3
Blé	10	12	15
Poisson	50	55	60

Nous pouvons calculer pour chaque période les valeurs aux prix courants ainsi que, pour les périodes 2 et 3, les valeurs aux prix de l'année précédente, c'est-à-dire les volumes :

Calcul des valeurs aux prix courants

		T1	T2	T3
Blé	Quantité	200	240	200
	Prix	10	12	15
	Valeur	2000	2880	3000
Poisson	Quantité	100	120	150
	Prix	50	55	60
	Valeur	5000	6600	9000
Total	Valeur	7000	9480	12000

Calcul des valeurs aux prix de l'année précédente

		T1	T2	T3
Blé	Quantité	-	240	200
	Prix	-	10	12
	Valeur	-	2400	2400
Poisson	Quantité	-	120	150
	Prix	-	50	55
	Valeur	-	6000	8250
Total	Valeur	-	8400	10650

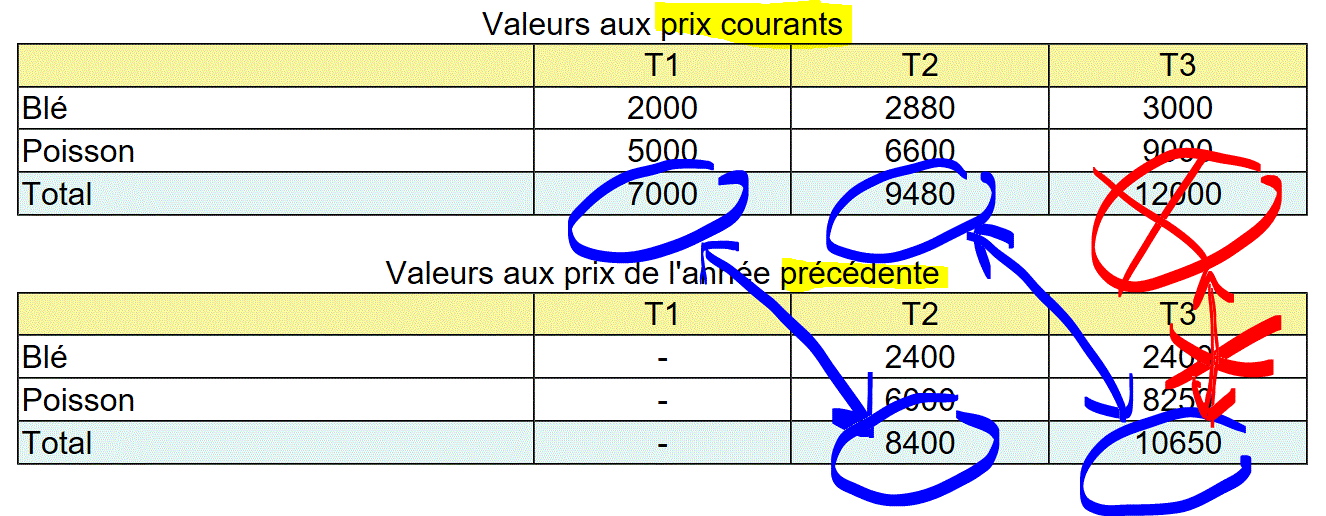
Pour calculer le taux de croissance de l'économie entre deux périodes il faut comparer la valeur de la première période au volume de la deuxième car tous deux ont été évalués aux mêmes prix.

Par exemple, entre la période 1 et la période 2, il faut comparer 7000 et 8400, ce qui donne un taux de croissance de 20%. Pour calculer le taux de croissance entre la période 2 et la période 3, il faut comparer 9480 et 10650, ce qui donne un taux de croissance de 12%.

Attention : il faut comparer le volume de l'année considérée à la valeur de l'année précédente. L'erreur classique est de comparer le volume d'une année à la valeur de cette même année.

Indices de volumes et de prix

Indices de volume

Le volume de la production correspond à la valeur qu'aurait eue la production de la période si les prix n'avaient pas changé depuis la période précédente. Cette grandeur n'aurait que peu d'intérêt si elle n'était comparée aux valeurs de l'année précédente. Pour exprimer l'évolution des quantités la comparaison doit porter sur des évaluations aux mêmes prix, c'est-à-dire le volume de la période et la valeur au prix courants de la période précédente.

Habituellement, les comptables nationaux utilisent des indices pour exprimer les évolutions. Un indice peut être défini par le rapport entre deux valeurs d'une même grandeur à deux périodes différentes, la période courante et la période de base :

Le plus souvent cet indice est multiplié par 100 pour ne pas faire apparaître un trop grand nombre de décimales, mais cette pratique complique les calculs et l'exposé, si bien que nous ne l'utiliserons pas.

Un indice de volume est donc obtenu en divisant le volume de la période courante par la valeur aux prix courants de la période de base.

Dans notre exemple précédent, les indices de volume exprimés en base 100 sont les suivants :

Indices de volume

	T1	T2	T3
Valeurs aux prix courants	7000	9480	12000
Valeurs aux prix de l'année précédente	-	8400	10650
Indices de volume	-	120,0	112,3

Indices de prix

Mais les comptes nationaux peuvent être utilisés non seulement pour mesurer la croissance à partir d'indices de volume mais également pour suivre l'évolution du niveau général des prix. En effet, dans une économie, les prix des produits suivent des évolutions diverses mais il peut être intéressant, notamment pour les autorités monétaires, de calculer un indice synthétique de prix qui permette d'évaluer l'inflation.

Un indice synthétique de prix peut être obtenu en généralisant la relation fondamentale du domaine des prix :

Valeur = prix × quantité

Cette relation qui est vraie pour un produit déterminé permet, si l'on connaît la valeur et la quantité d'en déduire le prix. Pour un ensemble de produits, il n'est pas possible d'utiliser directement les quantités mais il est possible d'utiliser le volume. Aussi, la relation précédente peut-elle être généralisée en remplaçant les quantités par les volumes et en l'exprimant sous la forme d'indices :

Indice de valeur = indice de prix × indice de volume

L'indice de valeur est égal au rapport entre la valeur de la période courante exprimée aux prix courants et la valeur de la période de base exprimée aux prix de la période de base. Ainsi, si l'on connaît l'indice de valeur et l'indice de volume, il est possible d'en déduire l'indice des prix :

L'indice des prix peut se calculer directement à partir des valeurs de la période aux prix courants et celles aux prix de l'année précédente car la valeur de la période précédente aux prix courants apparaît au dénominateur à la fois dans l'indice de valeur et dans l'indice de volume.

Ainsi, si nous reprenons l'exemple du blé et du poisson, les indices de prix sont les suivants :

Indices de volume et de prix

	T1	T2	T3
Valeurs aux prix courants	7000	9480	12000
Valeurs aux prix de l'année précédente	-	8400	10650
Indices de prix	-	112,9	112,7

Attention : contrairement à ce que nous avions fait pour le taux de croissance en volume, pour calculer un indice de prix, il faut comparer la valeur et le volume de la même année.

Indices de Laspeyres et indices de Paasche

L'indice de volume est un indice de Laspeyyres

Pour un ensemble de produits désignés par l'indice i, nous pouvons calculer des indices de volume et de prix. Nous désignerons pour cela l'exposant 0 pour désigner la période de base et l'exposant 1 pour désigner la période courante. Nous pouvons écrire :

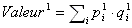
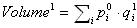
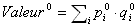
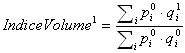
L'indice de volume est calculé en divisant la valeur de la période courante calculée aux prix de la période précédente par la valeur de la période précédente calculée aux prix de la période précédente. C'est-à-dire que l'indice de volume est calculé en figeant les prix dans le calcul des valeurs, les prix de la période précédente ayant été utilisés aussi bien pour le calcul de la valeur courante que pour celui de la période précédente.

On peut également écrire la formule de la manière suivante :

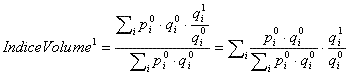
Dans cette dernière formule q¹_i/q⁰_i désigne l'indice élémentaire de quantité pour le produit i. Chaque indice élémentaire est multiplié par un coefficient qui représente la part de la valeur du produit i dans l'ensemble des produits à la période de base. Puisque la somme des coefficients est égale à 1, l'indice de volume est la moyenne arithmétique pondérée des indices élémentaires de quantité. Un indice calculé de cette manière est dit un indice de Laspeyres.

L'indice des prix est un indice de Paasche

L'indice de prix est calculé par le rapport entre l'indice de valeur et l'indice de volume, c'est-à-dire :

(Valeur¹/Valeur⁰)/(Volume¹/Valeur⁰) = Valeur¹/Volume¹ c'est-à-dire :

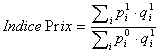
L'indice synthétique des prix est donc calculé en divisant la valeur de la période courante calculée aux quantités de la période courante par la valeur de la période précédente calculée aux quantités de la période courante. C'est-à-dire que les quantités ont été figées dans la comparaison des deux périodes, les quantités de la période courante ayant été utilisées à la fois pour le calcul de la valeur de la période courante et pour celui de la période précédente.

Il est intéressant de considérer l'inverse de cet indice, c'est-à-dire :

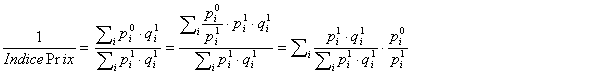
Dans cette dernière formule p⁰_i/p¹_i désigne l'inverse de l'indice élémentaire de prix pour le produit i. Chaque inverse d'indice élémentaire est multiplié par un coefficient qui représente la part de la valeur du produit i dans l'ensemble des produits à la période courante. Puisque la somme des coefficients est égale à 1, l'inverse de l'indice de prix est la moyenne des inverses des indices élémentaires de prix. Un indice calculé de cette manière est dit un indice de Paasche.

Les indices-chaînes

Les indices de Laspeyres et de Paasche ont en commun d'être très sensibles à la structure des valeurs à l'une des deux périodes, c'est-à-dire la période de base pour l'indice de Laspeyres, la période courante pour l'indice de Paasche. Lorsque ces deux périodes sont éloignées dans le temps, ces deux structures peuvent être très différentes, ce qui pose des problèmes.

Il est possible de calculer des volumes à partir des indices-chaînes en multipliant la valeur de la période de base par l'indice-chaîne de volume. Le problème avec les volumes obtenus de cette façon est que, contrairement aux valeurs calculées aux prix de l'année précédente, ils ne respectent pas l'équilibre des comptes.

Pour le montrer, reprenons notre exemple et supposons que le blé et le poisson sont produits dans le pays, que le blé est exporté et que le poisson est une consommation finale des ménages. On peut établir le compte de biens et services aux prix de l'année précédente, ainsi que le montre le tableau suivant :

		T1	T2	T3
Production	Valeur aux prix courants	7000	9480	12000
	Valeur aux prix de l'année précédente	-	8400	10650
	Indice de volume	-	1,200	1,123
Consommation finale	Valeur aux prix courants	5000	6600	9000
	Valeur aux prix de l'année précédente	-	6000	8250
	Indice de volume	-	1,200	1,250
Exportations	Valeur aux prix courants	2000	2880	3000
	Valeur aux prix de l'année précédente	-	2400	2400
	Indice de volume	-	1,200	0,833

On peut vérifier que l'équilibre du compte de biens et services est bien respecté aux prix de l'année de production pour les périodes T2 et T3, c'est-à-dire que la production est bien la somme de la consommation finale et des exportations.

De ce tableau on peut déduire des indices chaînes de volume pour comparer T1 et T3 en multipliant l'indice de volume aux prix de l'année précédente de T2 et T3. Ainsi, pour la production cet indice est égal à 1,200×1,123=1,348. On obtient le volume à la période T3 en multipliant la valeur à la période T1 par cet indice-chaîne. Pour la production, le volume à la période T3 est donc égal à 7000×1,348=9436,7. L'ensemble des volumes à la période T3 apparaît dans le tableau suivant :

	Valeur T1	Indice-chaîne	Volume T3
Production	7000	1,348	9436,7
Consommation finale	5000	1,500	7500,0
Exportations	2000	1,000	2000,0
Total emplois	7000		9500,0

On constate que le compte de biens et services en volume calculé à partir de l'indice-chaîne n'est pas équilibré car il existe un écart entre la somme des ressources et celle des emplois.

La valeur ajoutée

En toute rigueur, les notions de prix et de volume ne s'appliquent qu'à des opérations portant directement sur des produits pour lesquels on peut mesurer des quantités. On peut ainsi calculer le volume de la production, de la consommation intermédiaire, de la consommation finale, de la formation de capital, des importations et des exportations. À à l'inverse, on ne peut mesurer de volume pour les opérations de répartition parce qu'on ne peut pas leur associer de quantité.

La question se pose pour la valeur ajoutée, c'est une grandeur fondamentale pour la comptabilité nationale puisque c'est elle qui mesure la richesse créée par les hommes et, comme c'est une valeur monétaire, son évolution dépend elle aussi de celle des prix.

Pour mesurer la croissance de l'activité réelle, il est donc indispensable d'éliminer l'effet des fluctuations des prix dans l'évolution de la valeur ajoutée et donc de lui imputer un volume.

Pour cela, on peut considérer que la valeur ajoutée est égale à la différence entre la production et la consommation intermédiaire, deux grandeurs pour lesquelles il est possible de calculer un volume.

Par exemple considérons une boulangerie qui produit du pain à partir de farine, de levure, de sel et d'eau et d'énergie électrique. Sa valeur ajoutée aux prix courants est présentée dans le tableau suivant :

Valeurs aux prix courants

	T1	T2
Production	600	700
Consommation intermédiaire  - Farine  - Levure  - Sel  - Eau  - Électricité	240 80 15 5 46	260 90 16 6 51
Total consommation intermédiaire	386	423
Valeur ajoutée	214	277

Supposons que les indices de prix de base 100 à la période T1 soient les suivants à la période T2 :

Pain Farine Levure Sel Eau Électricité

109 108 105 106 104 106

La production et la consommation intermédiaire à la période T2 évaluées aux prix de la période T1 sont calculées en divisant les valeurs aux prix courants par les indices de prix. La valeur ajoutée aux prix de la période T1 est donc :

Valeurs aux prix de la période T1

	T1	T2
Production	600	642,2
Consommation intermédiaire  - Farine  - Levure  - Sel  - Eau  - Électricité	240 80 15 5 46	240,7 85,7 15,1 5,8 48,1
Total consommation intermédiaire	386	395,4
Valeur ajoutée	214	246,8

Pour calculer la croissance en volume de la valeur ajoutée, il faut comparer la valeur ajoutée de la période T2 évaluée aux prix de la période T1 à la valeur ajoutée aux prix courants de la période T1, c'est-à-dire calculer 246,8 / 214 = 1,153. On en déduit que la croissance du volume de la valeur ajoutée a été de 15,3% entre les deux périodes.

Cette méthode de calcul du volume de la valeur ajoutée est appelée la double déflation car elle consiste à déflater séparément la production et les consommations intermédiaires.

Les impôts et subventions sur les produits

Il est possible d'évaluer toutes les opérations sur biens et services en volume, si l'on veut élaborer le compte de biens et services et les équilibres ressources-emplois en volume, il est aussi nécessaire de calculer le volume des impôts et subventions sur les produits.

Il est possible de calculer le volume des impôts sur les produits car, selon leur définition, ce sont des impôts dus par unité de bien ou de service produite ou échangée. Il est donc possible de leur attribuer un prix qui est le montant de l'impôt prélevé par unité de biens et services et de calculer leur volume comme on l'a fait pour la production et les autres opérations sur biens et services.

Les impôts sur les produits peuvent être fixés de deux manières, soit comme un montant nominal fixe par unité de quantité du produit taxé, soit comme un certain pourcentage de la valeur de l’opération générant la taxation.

Dans le premier cas, le montant de la taxe par unité est le prix et il suffit d'appliquer la méthode habituelle.

Dans le second cas, pour calculer le montant de la taxe au prix de la période précédente, il faut multiplier les quantités taxées par le montant de la taxe unitaire à la période précédente. Concrètement, pour cela, le plus simple est de muliplier l'opération taxée évaluée aux prix de la période précédente par le taux de la période précédente.

Il faut également tenir compte des emplois puisque, par exemple, la TVA non déductible n'est pas la même pour la consommation intermédiaire des entreprises que pour la consommation finale des ménages. Le calcul doit donc être fait séparément pour chaque catégorie d'emploi.

Le raisonnement est le même pour les subventions sur les produits.

Les produits homogènes

Il n'est possible de définir des prix que pour des produits homogènes, c'est-à-dire des produits dont toutes les unités peuvent être considérées comme équivalentes. En effet, dans une économie de marché, si deux unités d'un produit sont considérées équivalentes, elles doivent avoir le même prix, ce prix qui est commun à l'ensemble de ses unités peut alors être attribué au produit lui-même. En revanche, si deux unités d'un produit ne sont pas équivalentes, elles doivent être considérées comme appartenant à deux produits différents.

Une autre manière de dire que deux unités d'un produit sont équivalentes est de dire qu'elles ont la même qualité, ainsi un produit homogène est constitué d'unités de même qualité. Cela implique que si deux unités sont de qualité différente, elles doivent être considérées comme appartenant à deux produits homogènes différents.

Lorsque la concurrence n'est pas parfaite, il est possible que deux unités d'un même produit considérées équivalentes par les clients soient, en fait, vendues à des prix différents. Par exemple, il est habituel de voir un même produit vendu dans deux points de vente différents sous des conditions identiques mais à des prix différents, simplement parce que les clients ont leurs habitudes et ne vérifient pas régulièrement le prix de tous les produits dans les différents points de vente.

Aussi, lorsque deux unités sont vendues à des prix différents mais auraient été vendues au même prix si la concurrence avait été parfaite, elles sont considérées équivalentes et donc appartenir au même produit homogène. Dans ce cas, le prix du produit homogène est défini comme le prix moyen de ses unités.

La comptabilité nationale considère ainsi que la qualité peut être définie à partir des facteurs suivants :

• caractéristiques physiques ;
• lieux de livraison différents ;
• moments de livraison différents - dans la journée ou l'année ;
• différences au niveau des conditions de vente, ou encore au niveau des circonstances ou du cadre dans lesquels sont fournis les biens ou services.

En effet, tous ces cas peuvent correspondre à des prix différents et cela même en situation de concurrence parfaite. Des différences dans ces facteurs correspondent ainsi à des produits homogènes différents.

Inversement, lorsque la différence de prix s'explique par un manque d'information, une discrimination limitant la liberté de choix des acheteurs ou l'existence d'un marché parallèle, on ne considèrera qu'un seul produit homogène dont le prix sera calculé par une moyenne.

La standardisation

Les produits homogènes n'existent habituellement pas naturellement mais ils sont le résultat d'un processus de standardisation. Ce processus garantit au produit un certain nombre de caractéristiques qui le définissent. Par exemple, les fruits peuvent être vendus par variété, comme la pomme golden ou la pomme gala, mais aussi par provenance, par taille, etc. L'important tant pour le vendeur que pour l'acheteur est que le produit soit suffisamment homogène pour qu'il ne soit pas nécessaire de discuter le prix de chaque pomme séparément.

La standardisation est extrêmement importante pour le comptable national car c'est elle qui permet le suivi de l'évolution des prix au cours du temps. En effet, supposons que l'on cherche à mesurer l'évolution des prix des pommes en un an en comparant les prix de septembre 2019 à ceux de septembre 2020. Cette comparaison ne peut se faire que pour des pommes de même qualité car on ne peut comparer une pomme golden de 2019 à une pomme gala de 2020. Mais comment peut-on s'assurer que les pommes dont on relève le prix en 2020 sont bien de la même qualité que celles dont on a relevé le prix en 2019 ? Une vérification directe est impossible car les pommes de 2019 n'existent plus en 2020.

La comparaison n'est rendue possible que par le processus de standardisation qui définit et maintient au cours du temps les caractéristiques précises des produits commercialisés. En fait, il serait impossible de mesurer l'évolution des prix et donc de calculer des taux de croissance en volume si la standardisation n'existait pas. Le problème, c'est que tous les produits ne font pas l'objet d'un processus de standardisation. De plus, l'apparition de nouveaux produits pose clairement un problème au comptable national.

Qualité et nouveaux produits

En pratique, les produits sont trop nombreux pour que les comptables nationaux puissent mesurer l'évolution des prix de chacun d'eux. Ils vont donc regrouper les produits présentant des caractéristiques proches en utilisant des nomenclatures de produits. Au sein de chaque classe de la nomenclature, ils vont sélectionner un échantillon de produits homogènes définis par leurs caractéristiques et vont en suivre l'évolution des prix. Ils pourront ainsi calculer un indice des prix et en déduire un indice de volume s'ils disposent d'un indice de valeur.

En procédant ainsi, ils supposent que l'évolution des prix des produits qu'ils ne suivent pas est parallèle à celle des produits qu'ils suivent. Cette hypothèse s'appuie sur le fait que les prix des produits sont largement déterminé par leurs coûts et que ceux-ci évoluent sous l'influence de facteurs qui, comme les salaires, sont communs à l'ensemble des produits d'une même classe de la nomenclature.

Un indice de volume retrace, en fait, non seulement l'évolution des quantités, mais aussi un effet de structure. Ainsi, dans l'exemple suivant, on considère deux variétés de pommes, la golden et la gala, dont les prix sont différents mais restent stables d'une période à l'autre :

		Golden	Gala	Total
T1	Quantité	20	10	30
	Prix	10	15	-
	Valeur	200	150	350
T2	Quantité	10	20	30
	Prix	10	15	-
	Valeur	100	300	400
	Volume	100	300	400

Ici l'indice de volume est égal à 400/350 = 1,14. Cette croissance du volume provient d'un effet de structure puisque ni les prix, ni les quantités globales n'ont changé. La valeur s'est accrue uniquement parce que la proportion de la variété de pommes la plus chère a augmenté. Cet effet de structure est souvent qualifié d'effet qualité, ce qui nous amène à préciser le sens que les comptables nationaux donnent au mot qualité.

Le terme qualité correspond d'abord, en comptabilité nationale, à une extension de la notion de variété. Par exemple, le mot "pommes" est un terme générique qui désigne certains fruits. La golden et la gala sont deux variétés de pommes aux caractéristiques bien définies. La comptabilité nationale va aller plus loin et tenir compte des autres facteurs physiques comme la taille, la couleur, ainsi que des lieux, des moments de livraison et des différences dans les conditions de vente, c'est-à-dire de l'ensemble des facteurs qui sont susceptibles d'influer sur le prix du produit.

Dire que la qualité d'un produit s'améliore signifie, pour le comptable national, que ce produit n'est pas homogène mais qu'il est constitué de différents produits homogènes dont la proportion en produits les plus chers s'accroît. En pratique, cette situation se présente lorsque les comptables nationaux calculent un indice de volume en divisant un indice de valeur par un indice de prix, ce qui est le cas le plus fréquent puisque la méthode directe de calcul du volume supposerait de connaître les quantités de chaque produit homogène.

Très souvent, l'effet qualité provient non seulement d'une modification de la composition en produits homogènes existants mais également de l'apparition de nouveaux produits. En général, les comptables nationaux ne se préoccupent pas de l'apparition de nouveaux produits car, si l'on s'en tient à la définition stricte des produits homogènes, des produits nouveaux apparaissent chaque jour.

Par exemple, l'apparition d'une nouvelle option pour une voiture devrait correspondre à l'apparition d'un nouveau produit homogène puisque le prix de la voiture avec et sans cette option est différent. Mais, en calculant l'indice de volume à partir d'un indice de valeur et d'un indice de prix mesuré à partir d'un échantillon de produits, le comptable national considère que toute variation de valeur qui ne provient pas d'une variation de son indice de prix correspond soit à une variation des quantités, soit à une modification de structure qu'il qualifie d'effet qualité, et il ne cherche pas à séparer ces deux facteurs.

En procédant ainsi, il suppose que les prix des produits ne figurant pas dans l'échantillon de produits utilisé pour le calcul de l'indice des prix évoluent comme cet indice, c'est-à-dire qu'il impute implicitement aux nouveaux produits des prix à la période de base correspondant à une évolution identique à celle de l'indice de prix utilisé. Par exemple, si l'indice des prix de voitures a augmenté de 10% entre la période de base et la période courante, le comptable national recalcule implicitement un prix de la voiture avec option pour la période de base en divisant le prix de la période courante par 1,10.

Les indices de prix hédoniques

Cette méthode de calcul des prix des nouveaux produits à la période de base est cependant remise en cause pour certains produits qui évoluent très rapidement, par exemple les ordinateurs. Dans ce cas, les comptables nationaux vont utiliser des indices de prix particuliers qualifiés d'indices de prix hédoniques. Les prix hédoniques ont été créés, à l'origine, pour déterminer le prix des biens immobiliers. En effet, il est rare de trouver deux biens immobiliers identiques si bien qu'une méthode intéressante pour évaluer le prix d'un bien particulier est de le déterminer à partir de ses caractéristiques.

Par exemple, le prix d'un logement dépend très largement d'un certain nombre de facteurs comme son nombre de pièces, sa superficie, son emplacement, etc. Des méthodes économétriques basées sur l'étude des caractéristiques et des prix des logements vendus vont permettre de déterminer quel poids à attribuer à chaque caractéristique dans la détermination du prix. Il devient alors possible d'estimer la valeur de marché de tout logement à partir de ses caractéristiques.

Cette méthode a été reprise pour évaluer le prix de certains nouveaux produits à la période de base. Par exemple, supposons que le prix d'un ordinateur soit déterminé à partir de la vitesse de son microprocesseur et de la capacité de son disque dur. Les méthodes économétriques permettent de reconstituer le prix de tout ordinateur à la période de base à partir de ces caractéristiques et donc de calculer le prix qu'aurait eu à la période de base un ordinateur qui n'est apparu qu'à la période courante. Il est dès lors possible de calculer un indice de prix et de l'utiliser pour déterminer un indice de volume.

En fait, les indices de prix hédoniques ont été utilisés parce qu'ils font apparaître dans le cas des ordinateurs des baisses de prix beaucoup plus importante que la méthode habituelle et qu'ils se traduisent donc par une croissance en volume beaucoup plus importante. On peut cependant se poser la question de la signification réelle des résultats obtenus par cette méthode.

Considérons, en effet, un pays où à la première période deux ordinateurs Ordi1 et Ordi2 sont en vente. L'ordinateur Ordi1 est très performant et vendu au prix de 100, l'ordinateur Ordi2 est beaucoup moins performant et vendu au prix de 50. Les quantités vendues sont de 20 pour l'ordinateur Ordi1 et de 80 pour l'ordinateur Ordi2.

Les acheteurs de l'ordinateur Ordi1 sont très attachés à la performance et insensibles au prix. Les acheteurs de l'ordinateur Ordi2 sont insensibles à la performance et choisissent toujours l'ordinateur le moins cher.

Supposons qu'à la deuxième période apparaisse l'ordinateur Ordi3 ayant les mêmes performances que l'ordinateur Ordi1 mais étant vendu au prix de l'ordinateur Ordi2. En conséquence, dans un souci de simplification, les vendeurs retirent du marché les ordinateurs Ordi1 et Ordi2. La quantité vendue de l'ordinateur Ordi3 à la deuxième période est de 100.

La valeur des ordinateurs au prix courants est à la première période de :

20 × 100 + 80 × 50 = 6000.

Si l'on applique la méthode hédonique pour calculer la croissance en volume, on va estimer à 100 le prix de l'ordinateur Ordi3 à la première période puisqu'il a les mêmes caractéristiques que l'ordinateur Ordi1.

Le volume à la deuxième période est calculé en appliquant aux quantités vendues de l'ordinateur Ordi3 son prix estimé à la première période. Il vaut donc :

100 × 10 = 10000 et l'indice de volume est égal à 10000 / 6000× 100 = 166,7.

Ainsi, l'application de la méthode hédonique fait apparaître une croissance importante du volume du marché des ordinateurs. Pourtant, entre les deux périodes, les quantités d'ordinateurs vendues sont les mêmes et aucun acheteur n'a ressenti la moindre amélioration. Le seul effet positif a été un effet prix mais il n'a concerné que les acheteurs qui y sont insensibles.

On peut donc douter que la méthode hédonique soit réellement toujours pertinente.

Les services non marchands

Les difficultés de mesure du volume dans le cas des services publics

Les services non marchands, c'est-à-dire l'essentiel des services publics et des services rendus par les institutions sans but lucratif, se caractérisent par le fait qu'ils sont mis à la disposition des usagers gratuitement ou à un prix non significatif car largement inférieur à leur coût de production. Dans ces conditions, soit il n'est pas possible de leur associer directement des prix, soit les prix ne reflètent aucunement les conditions de l'offre et de la demande. La méthode exposée précédemment pour le calcul du volume de la production ne peut donc s'appliquer directement car elle suppose l'existence de prix significatifs.

Mais l'inexistence de prix de marché n'est pas le seul problème dans le cas des services non marchands car il est souvent très difficile de définir des unités de quantité pour ces services. Par exemple, peut-on simplement définir des indices de quantité pour les services de défense nationale ou de police ?

Dans un premier temps, les comptables nationaux se sont donc orientés vers d'autres solutions. Puisque la valeur de la production des services non marchands est évaluée par la somme des coûts, ils ont calculé le volume de la production des services non marchands en divisant chaque élément du coût de la production par un indice de prix correspondant, c'est-à dire qu'is ont calculé les coûts aux prix de l'année précédente.

Cette méthode est la méthode input et c'est la seule qui ait été appliquée pendant des années par les comptables nationaux. Un exemple méthode input est donné dans le tableau suivant :

Volume de la production calculée par la méthode input

	Valeur aux prix courants	Indice de prix	Volume
Consommation intermédiaire	1200	1,04	1153,8
Rémunération des salariés	3500	1,06	3301,9
Consommation de capital fixe	800	1,02	784,3
Production	5500		5240,0

La méthode input présente l'inconvénient majeur de ne faire apparaître aucune évolution significative de la productivité. En effet, la mesure la plus courante de la productivité consiste à diviser le volume de la valeur ajoutée par le nombre d'heures travaillées. Or, la majeure partie de la valeur ajoutée des services publics est constituée de la rémunération des salariés, si bien que l'évolution de la valeur ajoutée reste quasiment parallèle à celle des salaires et ceci aussi bien aux prix constants qu'aux prix courants.

Dans ces conditions, si l'adoption de la méthode input pour les services publics permettait de résoudre le problème du calcul du volume de la production, elle n'était d'aucune utilité pour la mesure de la productivité. Pire, en supposant que les gains de productivité sont toujours nuls pour les services publics, elle pesait à la baisse sur la mesure de l'évolution des gains de productivité de l'économie nationale considérée dans son ensemble.

L'introduction des méthodes output

L'impossibilité de mesurer la productivité avec la méthode input a généré une pression de plus en plus forte pour l'adoption de nouvelles méthodes et ce tant de la part des économistes que des décideurs politiques. Puisque la mise en œuvre de la méthode input s'expliquait par le manque d'indicateurs de quantité pour les services publics, le premier effort porta sur la recherche de domaines pour lesquels il serait possible de définir des unités de quantité. Ainsi, parmi les services publics, deux catégories furent distinguées, les services publics collectifs et les services individuels.

Les services collectifs sont fournis simultanément à tous les membres de la communauté ou d'un de ses sous-groupes, ils comprennent, par exemple, les services de défense, de police et de justice. Ils se caractérisent notamment par le fait que leur fourniture à un individu ne réduit pas les quantités disponibles pour les autres individus. Au contraire, les services individuels sont acquis par les ménages dans le but de satisfaire les besoins de leurs membres, leur acquisition par un ménage excluant toute possibilité d'acquisition par d'autres ménages.

Pour les services collectifs il a été décidé de continuer, au moins dans un premier temps, d'appliquer la méthode input car la définition d'indicateurs de quantité pour ces services soulève trop de problèmes. L'une des principales difficultés relevées par les comptables nationaux réside dans le caractère préventif des services collectifs : le but de la police est la prévention des crimes, celui de l'armée la prévention de la guerre. Il apparaît dès lors difficile d'associer des quantités à ces services.

Pour les services individuels, des unités de quantité furent définies pour les services d'éducation et de santé. Ces unités sont définies à un niveau fin de la nomenclature d'activités, les principaux étant le nombre d'heures de cours suivies par les élèves dans le domaine de l'éducation et le nombre de traitements dispensés aux patients dans le cas des services de santé.

Dès lors que l'on a défini des unités de quantité pour ces services, il suffit de déterminer des prix pour pouvoir appliquer la méthode de calcul du volume. Pour cela, il est possible de raisonner par analogie avec le secteur marchand. Dans le domaine marchand, le prix d'un produit représente la quantité de monnaie que les consommateurs acceptent de dépenser pour acquérir une unité du produit, dans le secteur non marchand le coût unitaire d'un service correspond à la quantité de monnaie que les citoyens acceptent collectivement de dépenser pour acquérir ce produit. Ainsi, de ce point de vue, le coût unitaire d'un service non marchand peut être considéré comme son prix.

Puisque nous disposons de quantités et de prix, il est possible de calculer le volume de la production des services non marchands de l'éducation et de la santé en pondérant les quantités produites de chaque service par leur coût.

Cette méthode de calcul direct du volume à partir des unités de quantité et des prix est connue sous le nom de méthode output.

La question de la qualité

La mise en œuvre de la méthode output a cependant posé des problèmes dans certains pays. Ainsi, en Grande-Bretagne, l'augmentation des dépenses publiques de santé ne s'accompagnait pas d'un accroissement aussi important du volume de la production tel qu'il était mesuré par la méthode output, ce qui se traduisait par une dégradation de la productivité du service public de santé. La question s'est donc posée de savoir si cette dégradation apparente était bien réelle ou si elle s'expliquait par une inadéquation de l'instrument de mesure.

Dans le domaine des soins hospitaliers, par exemple, l'indicateur de quantité retenu est le nombre de traitements. Si le coût unitaire des traitements augmente ce n'est pas nécessairement parce que le service public de santé devient moins efficace, ce peut être simplement parce qu'un plus grand nombre de traitements coûteux sont dispensés. Si ces traitements coûteux sont également plus efficaces, c'est-à-dire de meilleure qualité, l'accroissement du coût moyen des traitements n'est pas nécessairement le signe d'une dégradation de la productivité du service de santé. C'est ainsi que s'est posé le problème de la qualité : il ne suffit pas de définir des indicateurs de quantité pour les services publics, il faut aussi tenir compte de leur qualité pour calculer correctement l'évolution de la productivité.

L'introduction de la notion de résultat (outcome)

Ainsi que nous l'avons vu, la question de la mesure du volume des services non marchands est étroitement liée à celle de la mesure de la productivité. L'introduction de la notion de résultat (outcome) vient de l'idée suivante : puisque la mesure du volume avec la méthode output ne permet pas de mesurer d'une manière satisfaisante la productivité, c'est-à-dire l'efficacité, déterminons directement par d'autres méthodes l'efficacité et nous pourrons en déduire une mesure du volume. L'avantage de cette approche était de pouvoir s'appuyer sur les nombreuses études consacrées à l'efficacité des services publics.

Trois niveaux sont ainsi définis. Le premier est la production, il correspond à l'activité des services publics, le deuxième est le résultat, le troisième l'utilité. Par exemple, dans le domaine de l'éducation, la production correspond au travail des professeurs, le résultat est le niveau scolaire des élèves. Dans le domaine de la santé, la production correspond au travail des médecins, le résultat est l'état de santé de la population. L'intérêt de la notion de résultat réside dans le fait que l'utilité est directement fonction du résultat et non de l'activité.

L'idée de base de la méthode basée sur le résultat, qualifiée de méthode outcome, est de définir la qualité des services non marchands à partir de leur résultat, ainsi deux unités de services publics seront considérées comme équivalentes si elles donnent le même résultat. Mais le niveau d'éducation et l'état de santé dépendent de nombreux facteurs et non seulement de l'action des services publics.

Aussi, le résultat de la production des services publics est-il défini non par la variation du niveau d'éducation ou de l'état de santé de la population, mais par la partie de cette variation s'expliquant par la seule action des services publics. Si l'on est capable de définir des indicateurs quantitatifs représentatifs, par exemple, du niveau d'éducation de la population, il est possible également par des méthodes économétriques de mesurer l'impact des services publics sur ces indicateurs et donc d'en déduire une évolution du volume de la production de services publics.

La méthode outcome n'a cependant pas réellement réussi à s'imposer et cela pour différentes raisons. Tout d'abord il est clair que les méthodes basées sur le résultat s'éloignent assez sensiblement des méthodes pratiquées dans le domaine des biens et services marchands. En effet, les méthodes basées sur le résultat supposent connus les objectifs que doivent atteindre les établissements publics et cherchent, en fait, à mesurer le degré de réalisation de ces objectifs. Par exemple, si un traitement destiné à combattre le cancer ne fait que guérir le rhume, on considérera que son résultat n'est pas satisfaisant. Son résultat aurait été positif s'il avait été destiné à combattre le rhume. On ne peut donc juger d'un résultat que par rapport à un objectif.

Dans le domaine marchand, la comptabilité nationale ne cherche jamais à déterminer quels sont les objectifs des différents agents économiques ni s'ils sont satisfaits, elle se contente de mesurer des prix et des volumes qui sont objectivement observables par les statisticiens.

La nécessité de préciser les objectifs poursuivis par les services publics est certainement le principal point faible de la méthode basée sur le résultat. Par exemple, quel est l'objectif du service de santé ? Allonger la durée de vie, lutter contre les maladies ? On voit bien qu'il est difficile, pour ne pas dire impossible de définir un objectif unique et si l'on accepte de reconnaître la multiplicité des objectifs se pose, pour le comptable national, le problème de leur pondération.

Par exemple, faut-il donner plus de poids à une année de vie en bonne santé qu'à deux années de vie en mauvaise santé ? Qui peut avoir la légitimité pour répondre à cette question ? Ainsi, l'expérience des pays européens engagés dans ces travaux a montré qu'il était pratiquement impossible de parvenir à un consensus sur la question des objectifs. De plus, même lorsqu'un accord pouvait être trouvé sur un objectif il était très difficile de déterminer un indicateur numérique pertinent pour le mesurer. Enfin, les méthodes basées sur le résultat font peser une lourde responsabilité sur les comptables nationaux car de leurs estimations peuvent dépendre des décisions importantes alors que les données de base susceptibles de les fonder sont extrêmement fragiles.

Auteur : Francis Malherbe

• Version PDF